Page 52 - Nature Of Space And Time

should not, therefore, be surprised that our region is homogeneous and isotropic and is
expanding at just the critical rate.
However, in
ation alone can not explain the present state of the universe. One can
see this by taking any state for the universe now and running it back in time. Providing it

contains enough matter, the singularity theorems will imply that there was a singularity
in the past. One can choose the initial conditions of the universe at the Big Bang to be the
initial conditions of this model. In this way, one can show that arbitrary initial conditions
at the Big Bang can lead to any state now. One can't even argue that most initial states

lead to a state like we observe today: the natural measure of both the initial conditions
that do lead to a universe like ours and those that don't is in nite. One can't therefore
claim that one is bigger than the other.
On the other hand, we saw in the case of gravity with a cosmological constant but no

matter elds that the no boundary condition could lead to a universe that was predictable
within the limits of quantum theory. This particular model did not describe the universe
we live in, which is full of matter and has zero or very small cosmological constant. However

one can get a more realistic model by dropping the cosmological constant and including
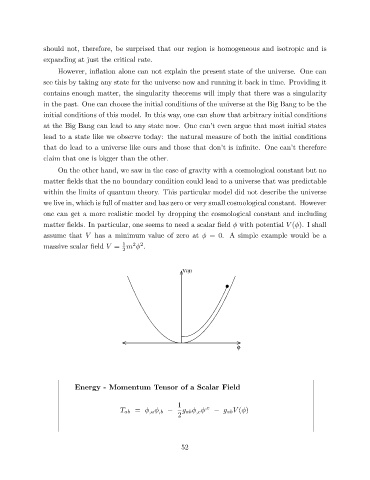
matter elds. In particular, one seems to need a scalar eld with potential V ( ). I shall
assume that V has a minimum value of zero at = 0. A simple example would be a
1
2 2
massive scalar eld V = m .
2

V(f)

f

Energy - Momentum Tensor of a Scalar Field

1 ;c
T ab = ;a ;b − g ab ;c − g abV ( )
2

52