Page 55 - Nature Of Space And Time

constant during the exponential expansion. When this happens the Schrodinger equation
will no longer be able to change the wave function fast enough that it can remain in the
ground state while the frequency changes. Instead it will freeze in the shape it had when
the frequency fell below the expansion rate.

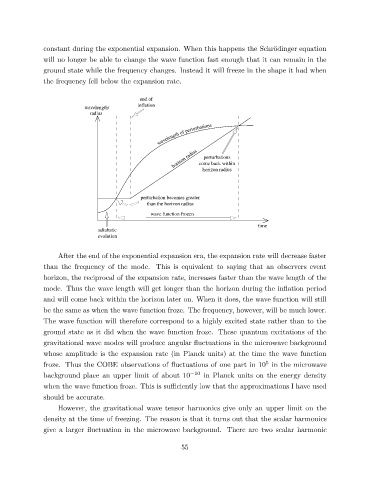
end of
inflation
wavelength/
radius
wavelength of perturbations

horizon radius come back within
perturbations

horizon radius

perturbation becomes greater
than the horizon radius
wave function frozen
time
adiabatic
evolution

After the end of the exponential expansion era, the expansion rate will decrease faster
than the frequency of the mode. This is equivalent to saying that an observers event

horizon, the reciprocal of the expansion rate, increases faster than the wave length of the
mode. Thus the wave length will get longer than the horizon during the in
ation period
and will come back within the horizon later on. When it does, the wave function will still
be the same as when the wave function froze. The frequency, however, will be much lower.

The wave function will therefore correspond to a highly excited state rather than to the
ground state as it did when the wave function froze. These quantum excitations of the
gravitational wave modes will produce angular
uctuations in the microwave background
whose amplitude is the expansion rate (in Planck units) at the time the wave function
5
froze. Thus the COBE observations of
uctuations of one part in 10 in the microwave
background place an upper limit of about 10 −10 in Planck units on the energy density
when the wave function froze. This is su ciently low that the approximations I have used
should be accurate.

However, the gravitational wave tensor harmonics give only an upper limit on the
density at the time of freezing. The reason is that it turns out that the scalar harmonics
give a larger
uctuation in the microwave background. There are two scalar harmonic

55