Page 153 - math 12

نيبراشلا نايبب تانايبلا ليثمت سردلا
ِ
Representation of Data by Box - whisker [ 7-2]
ﱠ
ملَعَت
ْ
َ
ِ
: ةيلاتلا طاقنلا ةارابم لك يف ةلسلا ةرك يبعلا دحأ لجس سردلا ُةْرـﱢكف
نايبب تانايبلا ليثمت •
، 38 ، 35 ، 40 ، 37 ، 35 نيبراشلا
نيبراشلا نيب ةنراقم •
40 ، 37 ، 42 ، 46 ، 46 تادرفملا
نيبراشلا نايب •

؟ نيبراشلا نايبب تانايبلا لثمأ فيك ىلعلاا عيبرلا •
ىندلأا عيبرلا •

يعيبرلا ىدملا •
Box and whisker Graph نيبراشلا نايب ]7-2-1[

طيسولا ، تاعيبرلا لامعتساب ، ماسقا ةعبرا ىلا اهبيترت دعب تانايبلا ميسقت بجي ، نيبراشلا نايب ىشنت يكل

ىندلأا عيبرلا ىلعلأا عيبرلا . ىلعا فصنو ىندلأا فصن ىلا تانايبلا مسقي طسولاا عيبرلا وا
ىندلاا عيبرلا وه : ىندلاا فصنلا يف طيسولا
رغصأ براشلا براشلا ربكأ
ةميق ىلعلاا عيبرلا وه : ىلعلاا فصنلا يف طيسولا
ةميق
طيسولا دادعلاا ميقتسم ىلع عزوت تاميسقتلا هذه

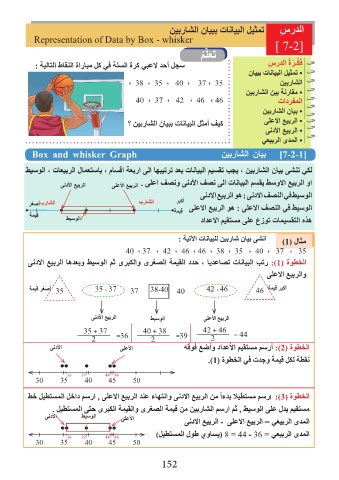
: ةيتلآا تانايبلل نيبراش نايب ىشنا
)1( لاثم
40 ، 37 ، 42 ، 46 ، 46 ، 38 ، 35 ، 40 ، 37 ، 35
ىندلاا عيبرلا اهدعبو طيسولا مث ىربكلاو ىرغصلا ةميقلا ددح ، ايدعاصت تانايبلا بتر :)1( ةوطخلا

ىلعلاا عيبرلاو

ةميق رغصأ 35 35 ، 37 37 38،40 40 42 ، 46 46 ةميق ربكأ

ىندلأا عيبرلا طيسولا ىلعلأا عيبرلا

35 + 37 40 + 38 42 + 46 = 44
2 =36 2 =39 2
ىندلأا ىلعلأا هقوف عضأو دادعلأا ميقتسم مسرأ :)2( ةوطخلا

.)1( ةوطخلا يف تدجو ةميق لكل ةطقن

36 39 44 46
30 35 40 45 50

طخ ليطتسملا لخاد مسرا , ىلعلاا عيبرلا دنع ءاهتناو ىندلاا عيبرلا نم أءدب لايطتسم مسرا :)3( ةوطخلا
. ليطتسملا ىتح ىربكلا ةميقلاو ىرغصلا ةميق نم نيبراشلا مسرا مث , طيسولا ىلع لدي ميقتسم
ىندلأا طيسولا ىلعلأا ىندلاا عيبرلا - ىلعلاا عيبرلا = يعيبرلا ىدملا

)ليطتسملا لوط يواسي( 8 = 44 - 36 = يعيبرلا ىدملا
36 39 44 46
30 35 40 45 50

152