Page 10 - NGTU_paper_withoutVideo

Modern Geomatics Technologies and Applications

LST of LDCM data aggregated to the same spatial resolution of the MODIS product using an 11 x 11 processing window size.
After scale up between the two sensors, for spectral and view zenith angle matching, the thermal homogeneity area was
determined. To this end, the co-occurrence matrix (CM) which contains a large amount of local spatial information about an
image is used. A set of texture features derived from the CM matrix was suggested by [46]. In particular, two texture features of
the inverse difference moment (IDM) and angular second moment (ASM) describe the homogeneity in an image. An 11 x 11
processing window size was selected and homogeneity measures were obtained. The processing window size is selected as
spatial resolution of MODIS is about ten times of LDCM thermal bands. Afterward, for time matching between LST of the
LDCM data and MODIS products. In this regard, the approximate overpass times of the Terra and Aqua satellites in study area
(scan start times from 01:30 to 24:00 UTC for MOD/ MYD 11_L2 and MOD/MYD 11 A1products) were considered during a
day. Usually, solar radiation changes during a day is almost a sine function. Accordingly, we modeled the pattern of surface
temperature changes during the day, as a sinusoidal function at a given point as Fig. 5.

Fig. 5. Time matching between LST of MODIS products and LDCM overpass for a validation point.
To evaluate the proposed LSE estimation methods, along with the SC algorithm, two statistical measures including, Mean
differences (MD), and RMSE were computed and given in Table 1.

Table 1.LST comparison with the conventional and proposed methods in homogeneity range (0.9-1.0)
Scenes N ANEM NBEM CBEM SRSC SEBAL Scenes VAvg CBVA
1st MD 35 1.67 K 1.16 K 1.12 K 1.82 K 1.16 K 1st MD 0.13 K 0.50 K
RMSE 2.44 K 2.37 K 2.59 K 2.61 K 2.67 K RMSE 1.78 K 1.94 K
2nd RMSE 63 1.35 K 1.19 K 1.66 K 1.12 K 1.65 K 2nd RMSE 0.38 K 0.53 K
MD
MD
2.11 K
1.71 K
2.03 K
1.65 K
2.38 K
2.33 K
1.96 K
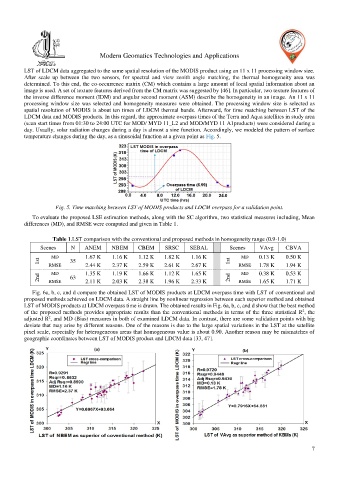
Fig. 6a, b, c, and d compare the obtained LST of MODIS products at LDCM overpass time with LST of conventional and
proposed methods achieved on LDCM data. A straight line by nonlinear regression between each superior method and obtained
LST of MODIS products at LDCM overpass time is drawn. The obtained results in Fig. 6a, b, c, and d show that the best method
2
of the proposed methods provides appropriate results than the conventional methods in terms of the three statistical R , the
adjusted R , and MD (Bias) measures in both of examined LDCM data. In contrast, there are some validation points with big
2
deviate that may arise by different reasons. One of the reasons is due to the large spatial variations in the LST at the satellite
pixel scale, especially for heterogeneous areas that homogeneous value is about 0.90. Another reason may be mismatches of
geographic coordinates between LST of MODIS product and LDCM data [33, 47].

7