Page 48 - Fundamentos de Física

VECTORES 39 yyy
4
4
3
2 2 vy=4
3 x1x1v=5x
v = 8.06 29.7°
vy=4
29.7° vx =7
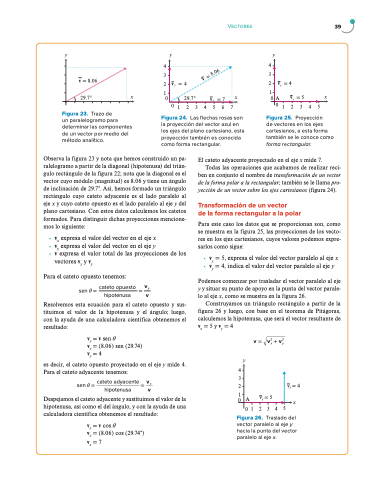
Figura 23. Trazo de
un paralelogramo para determinar las componentes de un vector por medio del método analítico.
0 0Ax 01234567 012345
Observa la figura 23 y nota que hemos construido un pa- ralelogramo a partir de la diagonal (hipotenusa) del trián- gulo rectángulo de la figura 22; nota que la diagonal es el vector cuyo módulo (magnitud) es 8.06 y tiene un ángulo de inclinación de 29.7°. Así, hemos formado un triángulo rectángulo cuyo cateto adyacente es el lado paralelo al eje x y cuyo cateto opuesto es el lado paralelo al eje y del plano cartesiano. Con estos datos calculemos los catetos formados. Para distinguir dichas proyecciones mencione- mos lo siguiente:
• vx expresa el valor del vector en el eje x
• vy expresa el valor del vector en el eje y
• v expresa el valor total de las proyecciones de los
vectores vx y vy
Para el cateto opuesto tenemos:
sen θ = cateto opuesto = vy hipotenusa v
Resolvemos esta ecuación para el cateto opuesto y sus- tituimos el valor de la hipotenusa y el ángulo; luego, con la ayuda de una calculadora científica obtenemos el resultado:
vy =vsenθ
El cateto adyacente proyectado en el eje x mide 7.
Todas las operaciones que acabamos de realizar reci- ben en conjunto el nombre de transformación de un vector de la forma polar a la rectangular; también se le llama pro-
yección de un vector sobre los ejes cartesianos (figura 24). Transformación de un vector
de la forma rectangular a la polar
Para este caso los datos que se proporcionan son, como se muestra en la figura 25, las proyecciones de los vecto- res en los ejes cartesianos, cuyos valores podemos expre- sarlos como sigue:
• vx = 5, expresa el valor del vector paralelo al eje x
• vy = 4, indica el valor del vector paralelo al eje y
Podemos comenzar por trasladar el vector paralelo al eje y y situar su punto de apoyo en la punta del vector parale- lo al eje x, como se muestra en la figura 26.
Construyamos un triángulo rectángulo a partir de la figura 26 y luego, con base en el teorema de Pitágoras, calculemos la hipotenusa, que será el vector resultante de
senθ=
= x v
vy = 4
vy = 4 y
y
es decir, el cateto opuesto proyectado en el eje y mide 4. Para el cateto adyacente tenemos:
4 3 2
Figura 24. Las flechas rosas son la proyección del vector azul en los ejes del plano cartesiano, esta proyección también es conocida como forma rectangular.
Figura 25. Proyección
de vectores en los ejes cartesianos, a esta forma también se le conoce como forma rectangular.
vx
= 5 y vy
= 4
v = (8.06) sen (29.74)
v= v2+v2 xy
cateto adyacente hipotenusa
v
Despejamos el cateto adyacente y sustituimos el valor de la hipotenusa, así como el del ángulo, y con la ayuda de una calculadora científica obtenemos el resultado:
vx =vcosθ
vx = (8.06) cos (29.74°)
vx = 7
1 v=5
0 Axx
012345
Figura 26. Traslado del vector paralelo al eje y hacia la punta del vector paralelo al eje x.
v = 8.06