Page 20 - UNI M4 Trigonometría_Neat

Trigonometría 5° UNI

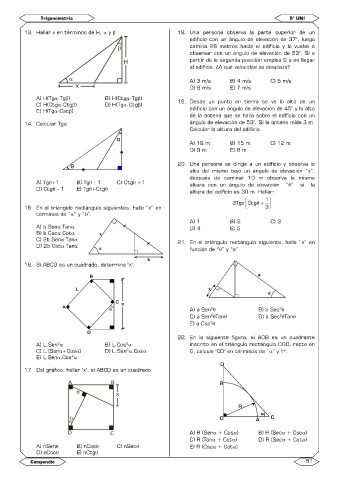
13. Hallar x en términos de H,  y  18. Una persona observa la parte superior de un
edificio con un ángulo de elevación de 37°, luego
camina 28 metros hacia el edificio y lo vuelve a
observar con un ángulo de elevación de 53°. Si a
partir de la segunda posición emplea 9 s en llegar
al edificio. ¿A qué velocidad se desplaza?

A) 3 m/s B) 4 m/s C) 5 m/s
D) 6 m/s E) 7 m/s

A) H(Tg-Tg) B) H(Ctg-Tg) 19. Desde un punto en tierra se ve lo alto de un
C) H(Ctg-Ctg) D) H(Tg-Ctg)
E) H(Tg-Csc) edificio con un ángulo de elevación de 45° y lo alto
de la antena que se halla sobre el edificio con un
14. Calcular Tg ángulo de elevación de 53°. Si la antena mide 3 m.
Calcular la altura del edificio.

A) 18 m B) 15 m C) 12 m
D) 9 m E) 8 m

20. Una persona se dirige a un edificio y observa lo
alto del mismo bajo un ángulo de elevación “x”;
después de caminar 10 m observa la misma
A) Tg+1 B) Tg - 1 C) Ctg +1 altura con un ángulo de elevación “” si la
D) Ctg - 1 E) Tg+Ctg altura del edificio es 30 m. Hallar:


3Tgx Ctg + 1 


15. En el triángulo rectángulo siguientes, halle “x” en  3
términos de “” y “b”.
A) 1 B) 2 C) 3
A) b Sen Tan D) 4 E) 5
B) b Csc Cot
C) 2b Sen Tan 21. En el triángulo rectángulo siguiente, halle “x” en
D) 2b Csc Tan
función de “” y “a”

16. Si ABCD es un cuadrado, determine "x".

2
A) a Sen  B) a Sec 
2
C) a Sen Tan D) a Sec Tan
2
2
2
E) a Csc 

22. En la siguiente figura, si AOB es un cuadrante
2
2
A) L.Sen  B) L.Cos  inscrito en el triángulo rectángulo COD, recto en
C) L.(Sen+Cos) D) L.Sen .Cos 0, calcule "CD" en términos de “” y "r".
2
E) L.Sen.Cos 
2

17. Del gráfico, hallar "x", si ABCD es un cuadrado.

A) R (Sen + Cos) B) R (Sec + Csc)
C) R (Tan + Cot) D) R (Sec + Cot)
A) nSen B) nCos C) nSec E) R (Csc + Cot)
D) nCsc E) nCtg

Compendio -81-