Page 12 - Ebookการวิเคราะห์ข้อมูล New

หนIวยการเรียนรูJที่ 3 การวิเคราะหKขJอมูล | 3.2 การวิเคราะหKเชิงทำนาย 3

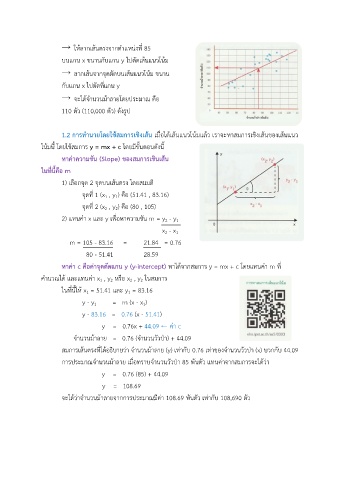
→ ให0ลากเส0นตรงจากตำแหน<งที่ 85

บนแกน x ขนานกับแกน y ไปตัดเส0นแนวโน0ม

→ ลากเส0นจากจุดตัดบนเส0นแนวโน0ม ขนาน

กับแกน x ไปตัดที่แกน y
→ จะได0จำนวนม0าลายโดยประมาณ คือ

110 ตัว (110,000 ตัว) ดังรูป

1.2 การทำนายโดยใชสมการเชิงเสFน เมื่อได0เส0นแนวโน0มแล0ว เราจะหาสมการเชิงเส0นของเส0นแนว
F
โน0มนี้ โดยใช0สมการ y = mx + c โดยมีขั้นตอนดังน ี้

หาคRาความชัน (Slope) ของสมการเชินเสFน
ในที่นี้คือ m

1) เลือกจุด 2 จุดบนเส0นตรง โดยสมมติ

จุดที่ 1 (x 1 , y 1) คือ (51.41 , 83.16)
จุดที่ 2 (x 2 , y 2) คือ (80 , 105)

2) แทนค<า x และ y เพื่อหาความชัน m = y 2 - y 1
x 2 - x 1

m = 105 - 83.16 = 21.84 = 0.76
80 - 51.41 28.59

หาคRา c คือคRาจุดตัดแกน y (y-intercept) หาได0จากสมการ y = mx + c โดยแทนค<า m ท ี่

คำนวณได0 และแทนค<า x 1 , y 2 หรือ x 2 , y 2 ในสมการ
ในที่นี้ให0 x 1 = 51.41 และ y 1 = 83.16

y - y 1 = m (x - x 1)

y - 83.16 = 0.76 (x - 51.41)
y = 0.76x + 44.09 ← ค<า c

จำนวนม0าลาย = 0.76 (จำนวนวัวปnา) + 44.09

สมการเส0นตรงที่ได0อธิบายว<า จำนวนม0าลาย (y) เท<ากับ 0.76 เท<าของจำนวนวัวปnา (x) บวกกับ 44.09
การประมาณจำนวนม0าลาย เมื่อทราบจำนวนวัวปnา 85 พันตัว แทนค<าจากสมการจะได0ว<า

y = 0.76 (85) + 44.09
y = 108.69

จะได0ว<าจำนวนม0าลายจากการประมาณมีค<า 108.69 พันตัว เท<ากับ 108,690 ตัว

เอกสารประกอบการเรียนรหัสวิชา ว 32103 รายวิชาวิทยาการคำนวณ 2 ชั้นมัธยมศึกษาปAที่ 5 | ครูธนเดช ลี้เลิศธนกุล