Page 54 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

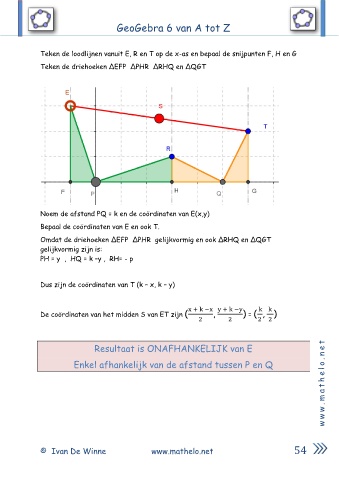
Teken de loodlijnen vanuit E, R en T op de x-as en bepaal de snijpunten F, H en G

Teken de driehoeken ∆EFP ∆PHR ∆RHQ en ∆QGT

Noem de afstand PQ = k en de coördinaten van E(x,y)
Bepaal de coördinaten van E en ook T.

Omdat de driehoeken ∆EFP ∆PHR gelijkvormig en ook ∆RHQ en ∆QGT

gelijkvormig zijn is:
PH = y , HQ = k –y , RH= - p

Dus zijn de coördinaten van T (k – x, k – y)

k k
De coördinaten van het midden S van ET zijn ( x + k −x y + k −y ) = ( , )
,
2 2 2 2

Resultaat is ONAFHANKELIJK van E t e
n
Enkel afhankelijk van de afstand tussen P en Q . o
l
e
h
t
a
m
.
w
w
w

© Ivan De Winne www.mathelo.net 54