Page 70 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

3.7 Kromme als unie van twee grafieken van functies

GeoGebra maakt het niet alleen mogelijk om grafieken van functies te tekenen,
door middel van het invoeren van het voorschrift van de functie f in het invoerveld,

maar voorziet bovendien verschillende opties om krommen weer te geven die niet
noodzakelijk de grafiek van een reële functie voorstellen.
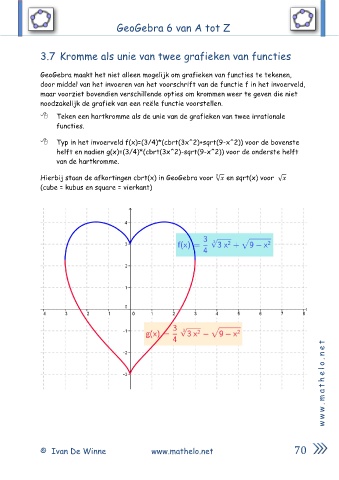
 Teken een hartkromme als de unie van de grafieken van twee irrationale
functies.

 Typ in het invoerveld f(x)=(3/4)*(cbrt(3x^2)+sqrt(9-x^2)) voor de bovenste
helft en nadien g(x)=(3/4)*(cbrt(3x^2)-sqrt(9-x^2)) voor de onderste helft
van de hartkromme.

Hierbij staan de afkortingen cbrt(x) in GeoGebra voor √ en sqrt(x) voor √
3
(cube = kubus en square = vierkant)

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© Ivan De Winne www.mathelo.net 70