Page 66 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

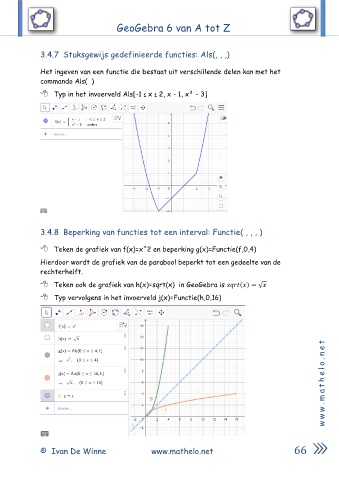
3.4.7 Stuksgewijs gedefinieerde functies: Als(, , ,)

Het ingeven van een functie die bestaat uit verschillende delen kan met het
commando Als( )

 Typ in het invoerveld Als[-1 ≤ x ≤ 2, x - 1, x² - 3]

3.4.8 Beperking van functies tot een interval: Functie( , , , )

 Teken de grafiek van f(x)=x^2 en beperking g(x)=Functie(f,0,4)
Hierdoor wordt de grafiek van de parabool beperkt tot een gedeelte van de
rechterhelft.

 Teken ook de grafiek van h(x)=sqrt(x) in GeoGebra is ( ) = √

 Typ vervolgens in het invoerveld j(x)=Functie(h,0,16)

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© Ivan De Winne www.mathelo.net 66