Page 64 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

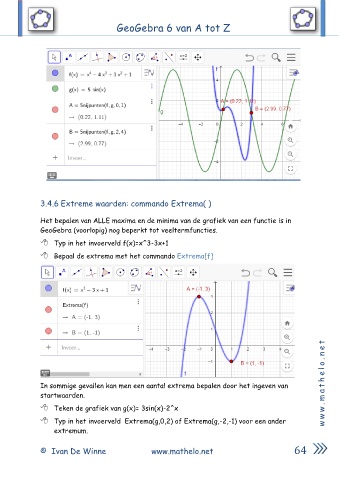
3.4.6 Extreme waarden: commando Extrema( )

Het bepalen van ALLE maxima en de minima van de grafiek van een functie is in
GeoGebra (voorlopig) nog beperkt tot veeltermfuncties.

 Typ in het invoerveld f(x)=x^3-3x+1

 Bepaal de extrema met het commando Extrema[f]

t
e
n
.
o
l
e
h
In sommige gevallen kan men een aantal extrema bepalen door het ingeven van t
startwaarden. a
m
 Teken de grafiek van g(x)= 3sin(x)-2^x . w

 Typ in het invoerveld Extrema(g,0,2) of Extrema(g,-2,-1) voor een ander w w
extremum.

© Ivan De Winne www.mathelo.net 64