Page 63 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

3.4.5 Snijpunten van 2 grafieken: commando Snijpunten( )

Het commando Snijpunten( ) kan enerzijds alle snijpunten bepalen van meetkundige
objecten zoals rechten en kegelsneden en ook de snijpunten van twee grafieken van
veeltermfuncties f en g.

Dit is ook mogelijk voor een beperkt aantal andere (niet) algebraïsche functies.
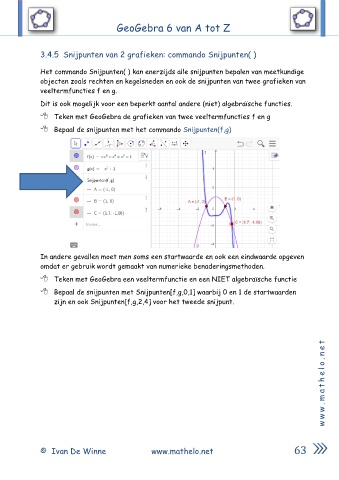
 Teken met GeoGebra de grafieken van twee veeltermfuncties f en g

 Bepaal de snijpunten met het commando Snijpunten(f,g)

In andere gevallen moet men soms een startwaarde en ook een eindwaarde opgeven
omdat er gebruik wordt gemaakt van numerieke benaderingsmethoden.

 Teken met GeoGebra een veeltermfunctie en een NIET algebraïsche functie

 Bepaal de snijpunten met Snijpunten[f,g,0,1] waarbij 0 en 1 de startwaarden
zijn en ook Snijpunten[f,g,2,4] voor het tweede snijpunt.

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© Ivan De Winne www.mathelo.net 63