Page 62 - Geogebra 6 van A tot Z
P. 62
GeoGebra 6 van A tot Z
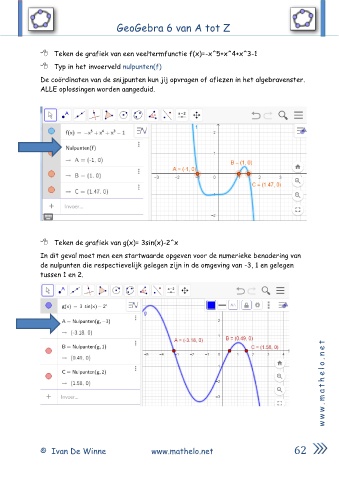
Teken de grafiek van een veeltermfunctie f(x)=-x^5+x^4+x^3-1
Typ in het invoerveld nulpunten(f)
De coördinaten van de snijpunten kun jij opvragen of aflezen in het algebravenster.
ALLE oplossingen worden aangeduid.
Teken de grafiek van g(x)= 3sin(x)-2^x
In dit geval moet men een startwaarde opgeven voor de numerieke benadering van
de nulpunten die respectievelijk gelegen zijn in de omgeving van -3, 1 en gelegen
tussen 1 en 2.
t
e
n
.
o
l
e
h
t
a
m
.
w w
w
© Ivan De Winne www.mathelo.net 62