Page 71 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

3.8 Functies met impliciet voorschrift

GeoGebra voorziet de mogelijkheid om grafieken van functies en krommen met
impliciete vergelijkingen weer te geven.

 Open een nieuw werkblad in Geogebra

 Typ vervolgens in het invoerveld de impliciete voorschriften van een parabool,
hyperbool en ook een ellips. Dit zijn de vergelijkingen van kegelsneden.

y^2=x x^2 - 4x*y - y^2- 3x + 2y = 1 en x^2/9 + y^2/13=1

Bij een eerste uitbreiding werden ook impliciete vergelijkingen van
veeltermvergelijkingen van een hogere graad dan 2 aanvaard.

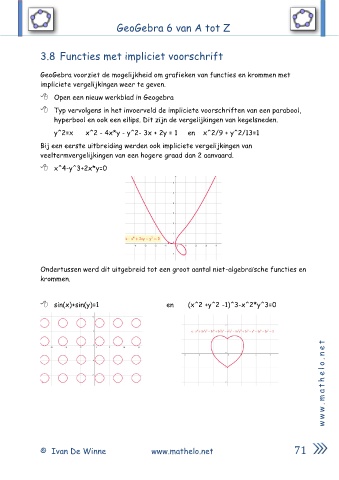
 x^4-y^3+2x*y=0

Ondertussen werd dit uitgebreid tot een groot aantal niet-algebraïsche functies en
krommen.

 sin(x)+sin(y)=1 en (x^2 +y^2 -1)^3-x^2*y^3=0

t
e
n
.
o
l
e
h t
a m

.
w
w
w

© Ivan De Winne www.mathelo.net 71