Page 76 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

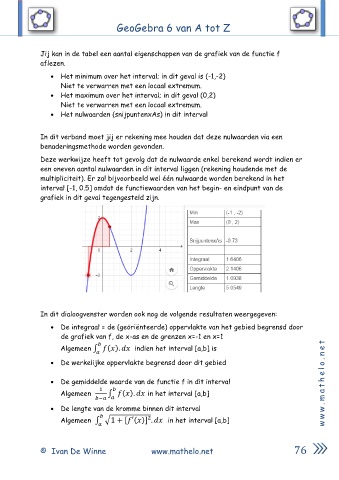
Jij kan in de tabel een aantal eigenschappen van de grafiek van de functie f
aflezen.

• Het minimum over het interval; in dit geval is (-1,-2)
Niet te verwarren met een locaal extremum.
• Het maximum over het interval; in dit geval (0,2)
Niet te verwarren met een locaal extremum.
• Het nulwaarden (snijpuntenxAs) in dit interval

In dit verband moet jij er rekening mee houden dat deze nulwaarden via een
benaderingsmethode worden gevonden.

Deze werkwijze heeft tot gevolg dat de nulwaarde enkel berekend wordt indien er
een oneven aantal nulwaarden in dit interval liggen (rekening houdende met de
multipliciteit). Er zal bijvoorbeeld wel één nulwaarde worden berekend in het
interval [-1, 0.5] omdat de functiewaarden van het begin- en eindpunt van de
grafiek in dit geval tegengesteld zijn.

In dit dialoogvenster worden ook nog de volgende resultaten weergegeven:
• De integraal = de (geöriënteerde) oppervlakte van het gebied begrensd door

de grafiek van f, de x-as en de grenzen x=-1 en x=1

Algemeen ∫ ( ). indien het interval [a,b] is t e
n
• De werkelijke oppervlakte begrensd door dit gebied . o
l e
• De gemiddelde waarde van de functie f in dit interval h

Algemeen 1 ∫ ( ). in het interval [a,b] t a
− m
• De lengte van de kromme binnen dit interval . w

Algemeen ∫ √1 + [ ′( )]². in het interval [a,b] w
w

© Ivan De Winne www.mathelo.net 76