Page 80 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

4.4.5 Afstand tussen twee punten met coördinaat

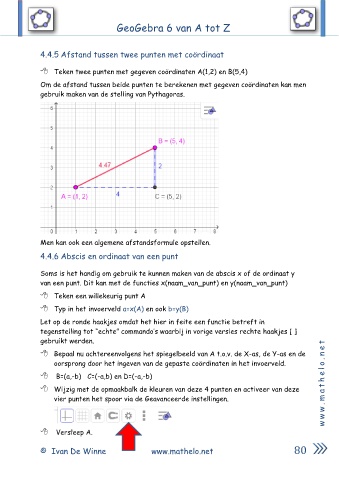
 Teken twee punten met gegeven coördinaten A(1,2) en B(5,4)
Om de afstand tussen beide punten te berekenen met gegeven coördinaten kan men

gebruik maken van de stelling van Pythagoras.

Men kan ook een algemene afstandsformule opstellen.

4.4.6 Abscis en ordinaat van een punt

Soms is het handig om gebruik te kunnen maken van de abscis x of de ordinaat y
van een punt. Dit kan met de functies x(naam_van_punt) en y(naam_van_punt)

 Teken een willekeurig punt A

 Typ in het invoerveld a=x(A) en ook b=y(B)
Let op de ronde haakjes omdat het hier in feite een functie betreft in

tegenstelling tot “echte” commando’s waarbij in vorige versies rechte haakjes [ ]
gebruikt werden. t
e
 Bepaal nu achtereenvolgens het spiegelbeeld van A t.o.v. de X-as, de Y-as en de n
oorsprong door het ingeven van de gepaste coördinaten in het invoerveld. . o
l
 B=(a,-b) C=(-a,b) en D=(-a,-b) e
h
 Wijzig met de opmaakbalk de kleuren van deze 4 punten en activeer van deze t a
vier punten het spoor via de Geavanceerde instellingen. m
.
w
w w

 Versleep A.

© Ivan De Winne www.mathelo.net 80