Page 83 - Geogebra 6 van A tot Z
P. 83
GeoGebra 6 van A tot Z
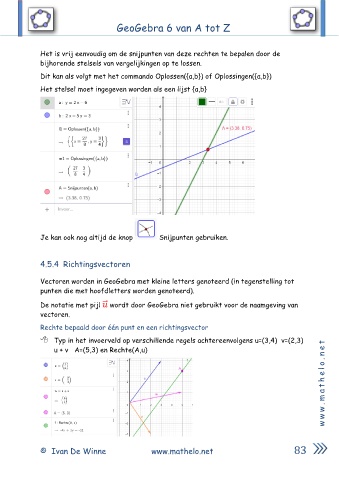
Het is vrij eenvoudig om de snijpunten van deze rechten te bepalen door de
bijhorende stelsels van vergelijkingen op te lossen.
Dit kan als volgt met het commando Oplossen({a,b}) of Oplossingen({a,b})
Het stelsel moet ingegeven worden als een lijst {a,b}
Je kan ook nog altijd de knop Snijpunten gebruiken.
4.5.4 Richtingsvectoren
Vectoren worden in GeoGebra met kleine letters genoteerd (in tegenstelling tot
punten die met hoofdletters worden genoteerd).
De notatie met pijl wordt door GeoGebra niet gebruikt voor de naamgeving van
⃗
vectoren.
Rechte bepaald door één punt en een richtingsvector
Typ in het invoerveld op verschillende regels achtereenvolgens u=(3,4) v=(2,3) t
u + v A=(5,3) en Rechte(A,u) e
n
.
o
l
e
h
t
a
m
.
w
w
w
© Ivan De Winne www.mathelo.net 83