Page 85 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

4.6 Cirkels

De algemene vorm van de (cartesiaanse) vergelijking van een cirkel met middelpunt
M(x1,y1) en straal R wordt gegeven door:

(x – x1)² + (y – y1)² = R²

Wij illustreren dit met een voorbeeld in GeoGebra

 Typ in het invoerveld de coördinaat van het middelpunt M = (3,5)

 Typ in het invoerveld de straal R = 2

Er wordt automatisch een Schuifknop aangemaakt waarmee het zal mogelijk zijn om
de straal van de cirkel te wijzigen.
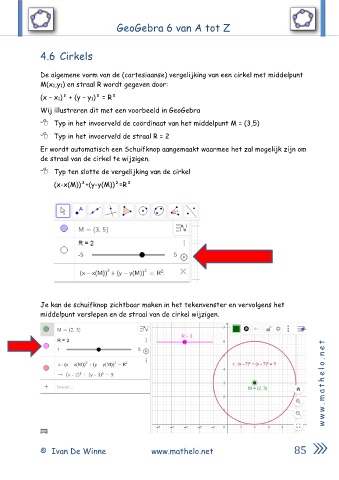
 Typ ten slotte de vergelijking van de cirkel

(x-x(M))²+(y-y(M))²=R²

Je kan de schuifknop zichtbaar maken in het tekenvenster en vervolgens het
middelpunt verslepen en de straal van de cirkel wijzigen.

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© Ivan De Winne www.mathelo.net 85