Page 89 - Geogebra 6 van A tot Z
P. 89
GeoGebra 6 van A tot Z
4.7 Ongelijkheden met GeoGebra
Een vergelijking van de vorm y=a.x + b verdeelt het vlak in 3 gebieden:
• Een halfvlak dat overeenkomt met de ongelijkheid y > a.x+b
• Een rechte met als vergelijking y = a.x+b
• Een halfvlak dat overeenkomt met y < a.x+b
Wij kunnen hierbij spreken over een bovengebied en een ondergebied.
In het geval van een verticale rechte x=c spreekt men over linker- en
rechtergebieden.
Het ingeven van ongelijkheden is in GeoGebra erg eenvoudig
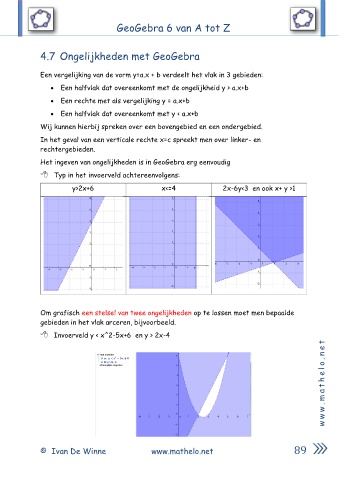
Typ in het invoerveld achtereenvolgens:
y>2x+6 x<=4 2x-6y<3 en ook x+ y >1
Om grafisch een stelsel van twee ongelijkheden op te lossen moet men bepaalde
gebieden in het vlak arceren, bijvoorbeeld.
Invoerveld y < x^2-5x+6 en y > 2x-4
t
e
n
.
o
l
e
h
t
a
m
.
w
w
w
© Ivan De Winne www.mathelo.net 89