Page 94 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

4.8.2 Schuifknop als parameter

Een schuifknop (slider) is ook een erg handig hulpmiddel om de invloed van een
parameter op de grafiek van een functie te onderzoeken…

Voorbeeld 1:
 Start GeoGebra en open een nieuw leeg werkblad.
Activeer ook het algebravenster.
Kies daartoe als schermindeling het Algebravenster en Tekenvenster.

 Maak een schuifknop a met
Hierbij is a een getal tussen -5 en 5 gelegen met Stapgrootte 0.1

 Wijzig de waarde van a door het verslepen van de schuifknop.

 Maak ook een schuifknop b tussen -5 en 5, stapgrootte 0.1.

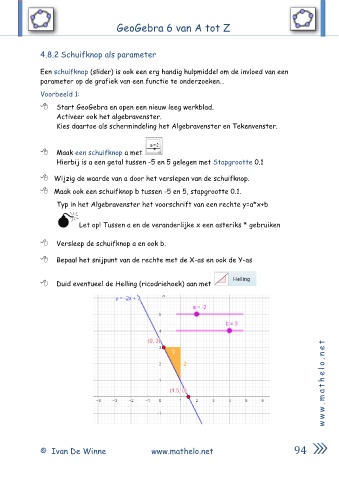
Typ in het Algebravenster het voorschrift van een rechte y=a*x+b

Let op! Tussen a en de veranderlijke x een asteriks * gebruiken

 Versleep de schuifknop a en ook b.

 Bepaal het snijpunt van de rechte met de X-as en ook de Y-as

 Duid eventueel de Helling (ricodriehoek) aan met

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© Ivan De Winne www.mathelo.net 94