Page 97 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

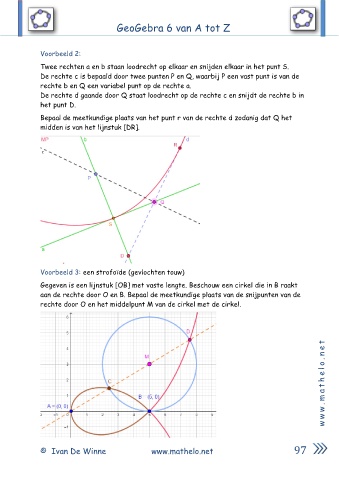
Voorbeeld 2:

Twee rechten a en b staan loodrecht op elkaar en snijden elkaar in het punt S.
De rechte c is bepaald door twee punten P en Q, waarbij P een vast punt is van de
rechte b en Q een variabel punt op de rechte a.
De rechte d gaande door Q staat loodrecht op de rechte c en snijdt de rechte b in
het punt D.

Bepaal de meetkundige plaats van het punt r van de rechte d zodanig dat Q het
midden is van het lijnstuk [DR].

Voorbeeld 3: een strofoïde (gevlochten touw)

Gegeven is een lijnstuk [OB] met vaste lengte. Beschouw een cirkel die in B raakt

aan de rechte door O en B. Bepaal de meetkundige plaats van de snijpunten van de
rechte door O en het middelpunt M van de cirkel met de cirkel.

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© Ivan De Winne www.mathelo.net 97