Page 95 - Geogebra 6 van A tot Z
P. 95
GeoGebra 6 van A tot Z
Voorbeeld 2: derdegraadsveelterm betekenis van parameter
Gegeven zijn een “familie” van veeltermfuncties van de derde graad.
f(x) = x³ + a x² - (a - 1) x + 5
Welke gemeenschappelijke kenmerken hebben deze functies?
Start GeoGebra en open een nieuw leeg werkblad.
Activeer ook het algebravenster.
Maak een schuifknop a met met -10 < a < 10 en stapgrootte 0.1
Typ in het algebravenster het voorschrift van f
f(x) = x^3 + a*x^2 - (a - 1)*x + 5
Versleep a.
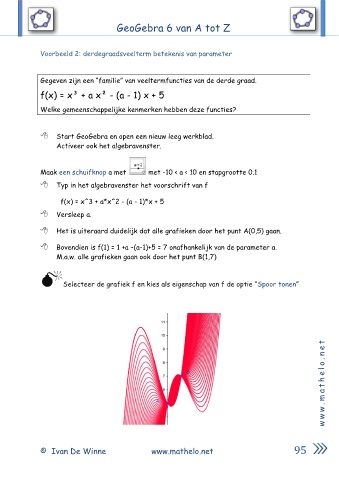
Het is uiteraard duidelijk dat alle grafieken door het punt A(0,5) gaan.
Bovendien is f(1) = 1 +a –(a-1)+5 = 7 onafhankelijk van de parameter a.
M.a.w. alle grafieken gaan ook door het punt B(1,7)
Selecteer de grafiek f en kies als eigenschap van f de optie “Spoor tonen”
t
e
n
.
o
l
e
h
t
a
m
.
w
w
w
© Ivan De Winne www.mathelo.net 95