Page 8 - Grafentheorie HS 2 Eulergrafen

HS 2 Grafentheorie

2.4 Koningsbergen “revisited”

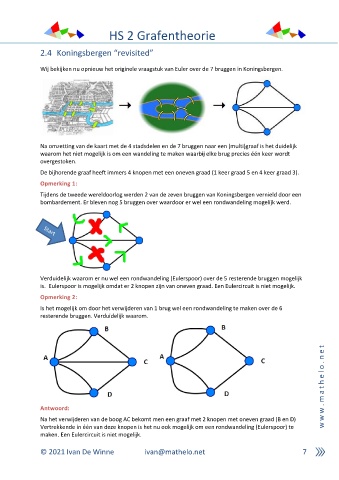
Wij bekijken nu opnieuw het originele vraagstuk van Euler over de 7 bruggen in Koningsbergen.

Na omzetting van de kaart met de 4 stadsdelen en de 7 bruggen naar een (multi)graaf is het duidelijk
waarom het niet mogelijk is om een wandeling te maken waarbij elke brug precies één keer wordt
overgestoken.
De bijhorende graaf heeft immers 4 knopen met een oneven graad (1 keer graad 5 en 4 keer graad 3).

Opmerking 1:
Tijdens de tweede wereldoorlog werden 2 van de zeven bruggen van Koningsbergen vernield door een
bombardement. Er bleven nog 5 bruggen over waardoor er wel een rondwandeling mogelijk werd.

Verduidelijk waarom er nu wel een rondwandeling (Eulerspoor) over de 5 resterende bruggen mogelijk
is. Eulerspoor is mogelijk omdat er 2 knopen zijn van oneven graad. Een Eulercircuit is niet mogelijk.
Opmerking 2:

Is het mogelijk om door het verwijderen van 1 brug wel een rondwandeling te maken over de 6
resterende bruggen. Verduidelijk waarom.

t
e
n
.
o
l
e
h
t
a
m
.
Antwoord:
w
Na het verwijderen van de boog AC bekomt men een graaf met 2 knopen met oneven graad (B en D) w
Vertrekkende in één van deze knopen is het nu ook mogelijk om een rondwandeling (Eulerspoor) te w
maken. Een Eulercircuit is niet mogelijk.

© 2021 Ivan De Winne ivan@mathelo.net 7