Page 4 - Grafentheorie HS 2 Eulergrafen

HS 2 Grafentheorie

2.2 Eulergrafen en de graden van de knopen

2.2.1 Graden van de knopen

Het opsporen van het bestaan van een Eulerspoor of een Eulercircuit in een graaf is niet zo eenvoudig.
De cruciale vraag hierbij is of je een wandeling kan maken waarbij je de bogen precies één keer passeert
(Eulerspoor) en of het mogelijk is de wandeling te eindigen in de startknoop (Eulercircuit).

Voor de voorbeelden van de getekende huisjes gaan wij na of het huisje in één keer kan getekend
worden zonder de pen op te heffen (Eulerspoor) of het huisje in één keer kan getekend worden zonder
de pen op te heffen waarbij men opnieuw eindigt in het startpunt.
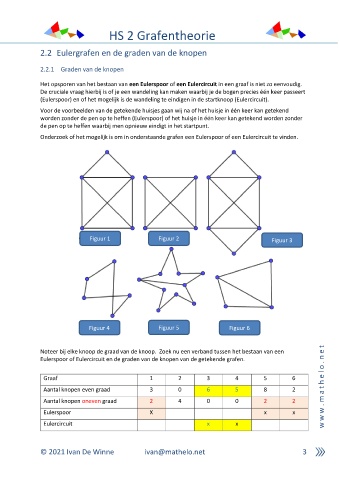
Onderzoek of het mogelijk is om in onderstaande grafen een Eulerspoor of een Eulercircuit te vinden.

Figuur 1 Figuur 2 Figuur 3

Figuur 4 Figuur 5 Figuur 6

t
Noteer bij elke knoop de graad van de knoop. Zoek nu een verband tussen het bestaan van een e
Eulerspoor of Eulercircuit en de graden van de knopen van de getekende grafen. n
.
o
l
Graaf 1 2 3 4 5 6 e
h
Aantal knopen even graad 3 0 6 5 8 2 t
a
Aantal knopen oneven graad 2 4 0 0 2 2 m
.
Eulerspoor X x x w
w
Eulercircuit x x w

© 2021 Ivan De Winne ivan@mathelo.net 3