Page 4 - HS 6 Grafieken van exp en log functies in de 3de graad

GeoGebra in de derde graad

6.3 Opgave 3: logaritmische functies met grondtal a

 Open het GeoGebra bestand logfct.ggb of via de link https://www.geogebra.org/m/txhwskbh

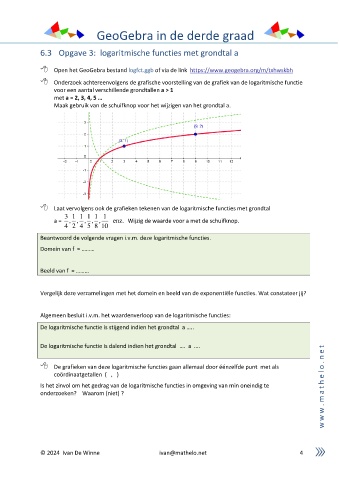
 Onderzoek achtereenvolgens de grafische voorstelling van de grafiek van de logaritmische functie
voor een aantal verschillende grondtallen a > 1
met a = 2, 3, 4, 5 …
Maak gebruik van de schuifknop voor het wijzigen van het grondtal a.

 Laat vervolgens ook de grafieken tekenen van de logaritmische functies met grondtal
3 1 1 1 1 1
a = , , , , , enz. Wijzig de waarde voor a met de schuifknop.
4 2 4 5 8 10

Beantwoord de volgende vragen i.v.m. deze logaritmische functies.
Domein van f = ………

Beeld van f = ………

Vergelijk deze verzamelingen met het domein en beeld van de exponentiële functies. Wat constateer jij?

Algemeen besluit i.v.m. het waardenverloop van de logaritmische functies:

De logaritmische functie is stijgend indien het grondtal a …..

De logaritmische functie is dalend indien het grondtal …. a …. t
e
n
.
 De grafieken van deze logaritmische functies gaan allemaal door éénzelfde punt met als o
coördinaatgetallen ( , ) l
e
h
Is het zinvol om het gedrag van de logaritmische functies in omgeving van min oneindig te t
onderzoeken? Waarom (niet) ? a
m
.
w

w
w

© 2024 Ivan De Winne ivan@mathelo.net 4