Page 4 - E MODUL
P. 4
A. JARAK TITIK KE TITIK PADA DIMENSI TIGA
Jarak antara dua titik adalah jarak terdekat yang menghubungkan ke dua buah titik
yang merupakan garis lurus, sehingga terbentuk saling tegak lurus dan dapat
diperhitungkan dengan teorema phytagoras.
Untuk lebih jelasnya perhatikan ilustrasi berikut ini!
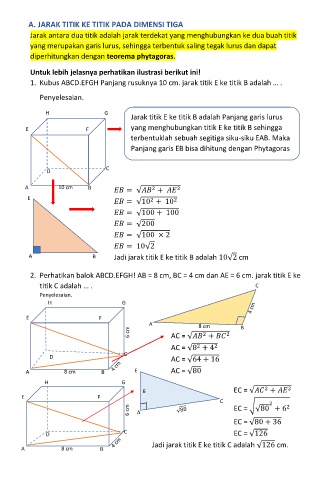
1. Kubus ABCD.EFGH Panjang rusuknya 10 cm. jarak titik E ke titik B adalah … .
Penyelesaian.
H G
Jarak titik E ke titik B adalah Panjang garis lurus
E F yang menghubungkan titik E ke titik B sehingga
terbentuklah sebuah segitiga siku-siku EAB. Maka
Panjang garis EB bisa dihitung dengan Phytagoras
C
D
A 10 cm B 2 2
= √ +
E 2 2
= √10 + 10
= √100 + 100
= √200
= √100 × 2
= 10√2
A B Jadi jarak titik E ke titik B adalah 10√2 cm
2. Perhatikan balok ABCD.EFGH! AB = 8 cm, BC = 4 cm dan AE = 6 cm. jarak titik E ke
titik C adalah … . C
Penyelesaian.
H G
E F
A 8 cm B
6 cm AC = √ +
2
2
2
2
AC = √8 + 4
C
D AC = √64 + 16
A 8 cm B E AC = √80
H G
2
2
6 EC = √ +
E F
C 2
√
6 cm A EC = √80 + 6
2
EC = √80 + 36
C
D EC = √126
Jadi jarak titik E ke titik C adalah √126 cm.
A 8 cm B