Page 10 - e-MODUL-Teorema-Pythagoras latihan
P. 10
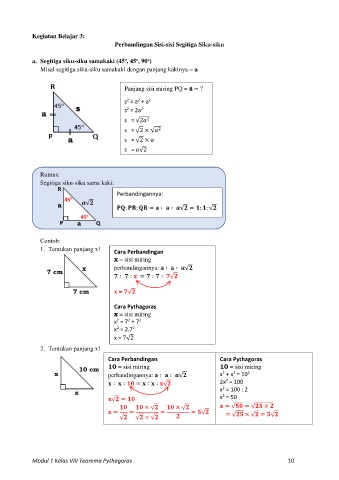
Kegiatan Belajar 3:
Perbandingan Sisi-sisi Segitiga Siku-siku
o
o
o
a. Segitiga siku-siku samakaki (45 , 45 , 90 )
Misal segitiga siku-siku samakaki dengan panjang kakinya = a
Panjang sisi miring PQ = s = ?
2
2
2
s = a + a
2
2
s = 2a
2
s = √2
2
s = √2 × √
s = √2 ×
s = √2
Rumus:
Segitiga siku-siku sama kaki:
R Perbandingannya:
45 √
o
a : : = ∶ ∶ √ = : : √
45
o
P a Q
Contoh:
1. Tentukan panjang x! Cara Perbandingan
x = sisi miring
x perbandingannya: ∶ ∶ √
7 cm ∶ ∶ = ∶ ∶ √
7 cm x = √
Cara Pythagoras
x = sisi miring
2
2
2
x = 7 + 7
2
2
x = 2.7
x = 7√2
2. Tentukan panjang x!
Cara Perbandingan Cara Pythagoras
10 = sisi miring 10 = sisi miring
x 10 cm perbandingannya: ∶ ∶ √ x + x = 10
2
2
2
∶ ∶ = ∶ ∶ √ 2x = 100
2
2
x x = 100 : 2
2
√ = x = 50
× √ × √ = √ = √ ×
= √ = √ × √ = = √ = √ × √ = √
Modul 1 Kelas VIII Teorema Pythagoras 10