Page 21 - Производная_removed (1)_Neat

Выясним характер критических точек. Для этого с помощью метода интервалов расставляем
знаки производной и определяем промежутки возрастания и убывания (рис. 16).

− − +
0 3 X

4
Рис. 16. Поведение функции f(x) = x − 4x 3

При переходе через точку x = 0 производная не меняет знака: функция убывает как на
промежутке (−∞, 0], так и на промежутке [0, 3]. Поэтому точка x = 0 является седловой точкой
функции.
А вот при переходе через точку x = 3 производная меняет знак с (−) на (+). На проме-
жутке [3, +∞) функция возрастает, а точка x = 3 служит точкой минимума. Значение в точке
минимума: f(3) = −27.
Найдём точки пересечения с осью X:

3
3
4
x − 4x = 0 ⇒ x (x − 4) = 0.
Значит, ось X пересекается в точках x = 0 (а это седловая точка) и x = 4. Остаётся построить
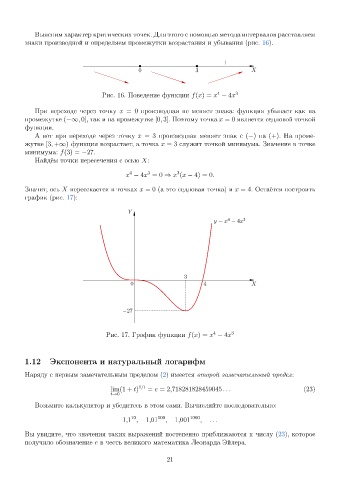
график (рис. 17):

Y
4
y = x − 4x 3

3
0 4 X

−27

4
Рис. 17. График функции f(x) = x − 4x 3

1.12 Экспонента и натуральный логарифм

Наряду с первым замечательным пределом (2) имеется второй замечательный предел:

lim(1 + t) 1/t = e = 2,718281828459045 . . . (23)
t→0
Возьмите калькулятор и убедитесь в этом сами. Вычисляйте последовательно:

10
1,1 , 1,01 100 , 1,001 1000 , . . .

Вы увидите, что значения таких выражений постепенно приближаются к числу (23), которое
получило обозначение e в честь великого математика Леонарда Эйлера.

21