Page 17 - Производная_removed (1)_Neat

Однако не следует думать, что непрерывная функция не дифференцируема только в точках
излома, то есть там, где отсутствует касательная. Может случиться, что касательную к графику
функции провести можно, но, тем не менее, производная функции в этой точке не существует.
Соответствующий пример показан на рис. 9.

Y
y = f(x)

C

X
x 0

Рис. 9. Касательная есть, а производной нет

В точке C касательная имеется, но она перпендикулярна оси X. Угол наклона касательной
0
◦
ϕ = 90 , поэтому tg ϕ не существует. Следовательно, не существует и f (x 0 ).
В этом случае перестаёт быть справедливым и уравнение касательной (22), поскольку каса-
тельная на рис. 9 не имеет углового коэффициента. Уравнение данной касательной выглядит
так: x = x 0 .
√
Упражнение. Напишите уравнение касательной к графику функции y = 3 x в точке (0, 0).

1.11 Исследование функций

Все функции, которые рассматриваются нами далее, считаются дифференцируемыми в нужных
точках. Поэтому существование касательных подразумевается по умолчанию.
На рис. 10 изображён график функции y = f(x) и проведены касательные в двух точках с
абсциссами x 1 и x 2 .

ϕ 2
ϕ 1
X
x 1 x 2
y = f(x)
0
0
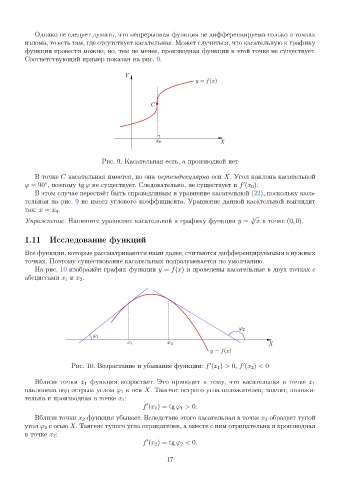
Рис. 10. Возрастание и убывание функции: f (x 1 ) > 0, f (x 2 ) < 0

Вблизи точки x 1 функция возрастает. Это приводит к тому, что касательная в точке x 1
наклонена под острым углом ϕ 1 к оси X. Тангенс острого угла положителен; значит, положи-
тельна и производная в точке x 1 :
0
f (x 1 ) = tg ϕ 1 > 0.
Вблизи точки x 2 функция убывает. Вследствие этого касательная в точке x 2 образует тупой
угол ϕ 2 с осью X. Тангенс тупого угла отрицателен, а вместе с ним отрицательна и производная
в точке x 2 :
0
f (x 2 ) = tg ϕ 2 < 0.

17