Page 15 - Производная_removed (1)_Neat

Вспомним ещё, что тангенс угла наклона прямой это её угловой коэффициент, то есть
число k в уравнении прямой y = kx + b. Тем самым:

0
f (x 0 ) = tg ϕ = k. (20)
Мы пришли к этому выводу, пользуясь графиком возрастающей функции. Что изменится,
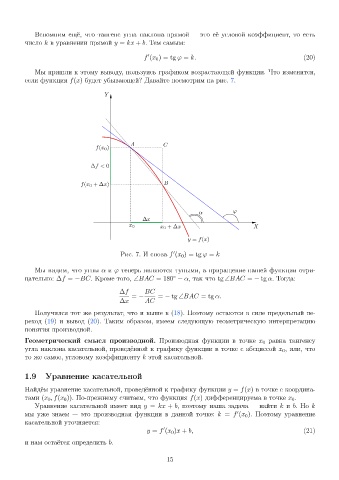
если функция f(x) будет убывающей? Давайте посмотрим на рис. 7.

Y

A C
f(x 0 )

∆f < 0

f(x 0 + ∆x) B

α ϕ
∆x
x 0 x 0 + ∆x X

y = f(x)

0
Рис. 7. И снова f (x 0 ) = tg ϕ = k

Мы видим, что углы α и ϕ теперь являются тупыми, а приращение нашей функции отри-
◦
цательно: ∆f = −BC. Кроме того, ∠BAC = 180 − α, так что tg ∠BAC = − tg α. Тогда:
∆f BC
= − = − tg ∠BAC = tg α.
∆x AC

Получился тот же результат, что и выше в (18). Поэтому остаются в силе предельный пе-
реход (19) и вывод (20). Таким образом, имеем следующую геометрическую интерпретацию
понятия производной.
Геометрический смысл производной. Производная функции в точке x 0 равна тангенсу
угла наклона касательной, проведённой к графику функции в точке с абсциссой x 0 , или, что
то же самое, угловому коэффициенту k этой касательной.

1.9 Уравнение касательной

Найдём уравнение касательной, проведённой к графику функции y = f(x) в точке с координа-
тами (x 0 , f(x 0 )). По-прежнему считаем, что функция f(x) дифференцируема в точке x 0 .
Уравнение касательной имеет вид y = kx + b, поэтому наша задача найти k и b. Но k
0
мы уже знаем это производная функции в данной точке: k = f (x 0 ). Поэтому уравнение
касательной уточняется:
0
y = f (x 0 )x + b, (21)
и нам остаётся определить b.

15