Page 18 - Производная_removed (1)_Neat
P. 18
Справедливы также и обратные утверждения.
Признак возрастания функции. Если производная положительна на некотором промежут-
ке, то функция возрастает на этом промежутке.
Признак убывания функции. Если производная отрицательна на некотором промежутке,
то функция убывает на этом промежутке.
В самом деле, если скорость изменения количества ваших денег положительна, то денег
у вас прибавляется. А вот если скорость наполнения кошелька отрицательна, то денег в нём
становится меньше :-)
Наблюдение за знаком производной лежит в основе исследования функций. Рассмотрим,
например, функцию
3
f(x) = x − 3x.
Выясним, на каких промежутках эта функция возрастает, а на каких убывает. Для этого
находим её производную:
0
2
f (x) = 3x − 3 = 3(x + 1)(x − 1).
Методом интервалов определяем знаки производной и отмечаем стрелками возрастание или
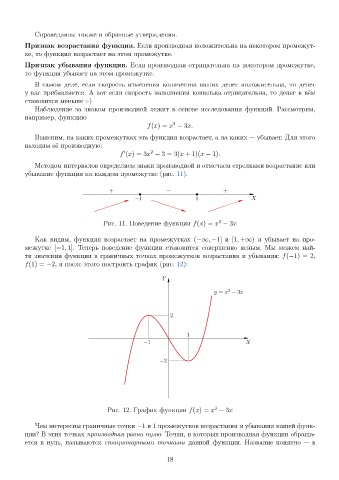
убывание функции на каждом промежутке (рис. 11).
+ − +
−1 1 X
3
Рис. 11. Поведение функции f(x) = x − 3x
Как видим, функция возрастает на промежутках (−∞, −1] и [1, +∞) и убывает на про-
межутке [−1, 1]. Теперь поведение функции становится совершенно ясным. Мы можем най-
ти значения функции в граничных точках промежутков возрастания и убывания: f(−1) = 2,
f(1) = −2, и после этого построить график (рис. 12):
Y
3
y = x − 3x
2
1
−1 X
−2
3
Рис. 12. График функции f(x) = x − 3x
Чем интересны граничные точки −1 и 1 промежутков возрастания и убывания нашей функ-
ции? В этих точках производная равна нулю. Точки, в которых производная функции обраща-
ется в нуль, называются стационарными точками данной функции. Название понятно в
18