Page 67 - Turunan Fungsi Aljabar.prototype1

55

Uraian Materi

A. Hubungan antara titik stasioner dengan turunan kedua
fungsi

Bagaimana hubungan antara titik stasioner dengan turunan kedua
fungsi?

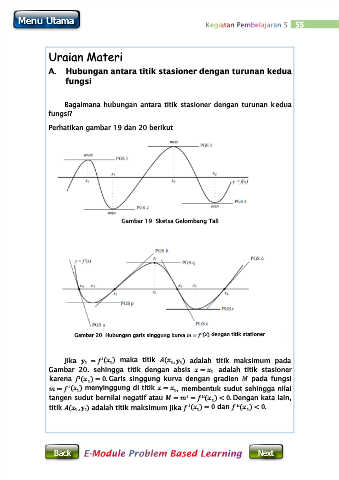
Perhatikan gambar 19 dan 20 berikut

Gambar 19. Sketsa Gelombang Tali

′
Gambar 20. Hubungan garis singgung kurva = ( ) dengan titik stationer

Jika = ( ) maka titik ( , ) adalah titik maksimum pada
′
1
1
1
1
Gambar 20. sehingga titik dengan absis = adalah titik stasioner
1
karena ( ) = 0. Garis singgung kurva dengan gradien pada fungsi
′
1
′
= ( ) menyinggung di titik = , membentuk sudut sehingga nilai
1
1
tangen sudut bernilai negatif atau = = ( ) < 0. Dengan kata lain,
′
′′
1
′′
titik ( , ) adalah titik maksimum jika ( ) = 0 dan ( ) < 0.
′
1
1
1
1