Page 7 - ET_GREL_Tabellen

ARBEITSHEFT – ELEKTROTECHNIK – TABELLEN SEITE 7

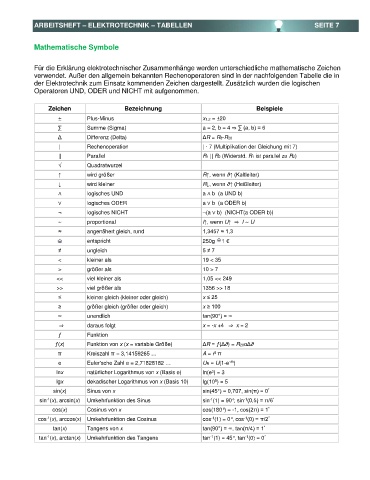
Mathematische Symbole

Für die Erklärung elektrotechnischer Zusammenhänge werden unterschiedliche mathematische Zeichen
verwendet. Außer den allgemein bekannten Rechenoperatoren sind in der nachfolgenden Tabelle die in
der Elektrotechnik zum Einsatz kommenden Zeichen dargestellt. Zusätzlich wurden die logischen
Operatoren UND, ODER und NICHT mit aufgenommen.

Zeichen Bezeichnung Beispiele
± Plus-Minus x1,2 = ±20
∑ Summe (Sigma) a = 2, b = 4 ⇒ ∑ (a, b) = 6
Δ Differenz (Delta) ΔR = Rϑ-R20
| Rechenoperation | · 7 (Multiplikation der Gleichung mit 7)
|| Parallel R1 || R2 (Widerstd. R1 ist parallel zu R2)
√ Quadratwurzel
↑ wird größer R↑, wenn ϑ↑ (Kaltleiter)
↓ wird kleiner R↓, wenn ϑ↑ (Heißleiter)
∧ logisches UND a ∧ b (a UND b)
∨ logisches ODER a ∨ b (a ODER b)
¬ logisches NICHT ¬(a ∨ b) (NICHT(a ODER b))
∼ proportional I↑, wenn U↑ ⇒ I ∼ U
≈ angenähert gleich, rund 1,3457 ≈ 1,3
entspricht 250g 1 €

≠ ungleich 5 ≠ 7
< kleiner als 19 < 35
> größer als 10 > 7
<< viel kleiner als 1,05 << 249
>> viel größer als 1356 >> 18
≤ kleiner gleich (kleiner oder gleich) x ≤ 25
≥ größer gleich (größer oder gleich) x ≥ 100
∞ unendlich tan(90°) = ∞
⇒ daraus folgt x = -x +4 ⇒ x = 2
ƒ Funktion
ƒ(x) Funktion von x (x = variable Größe) ΔR = ƒ(Δϑ) = R20αΔϑ
π Kreiszahl π = 3,14159265 … A = r² π
e Euler'sche Zahl e = 2,71828182 … UR = U(1-e )
-t/τ
lnx natürlicher Logarithmus von x (Basis e) ln(e³) = 3
lgx dekadischer Logarithmus von x (Basis 10) lg(10 ) = 5
5
*
sin(x) Sinus von x sin(45°) = 0,707, sin(π) = 0
-1
-1
sin (x), arcsin(x) Umkehrfunktion des Sinus sin (1) = 90°, sin (0,5) = π/6 *
-1
*
cos(x) Cosinus von x cos(180°) = -1, cos(2π) = 1
-1
-1
cos (x), arccos(x) Umkehrfunktion des Cosinus cos (1) = 0°, cos (0) = π/2
*
-1
tan(x) Tangens von x tan(90°) = ∞, tan(π/4) = 1 *
*
-1
tan (x), arctan(x) Umkehrfunktion des Tangens tan (1) = 45°, tan (0) = 0
-1
-1