Page 4 - BOOK TRANSFORMASI (11 HAL)

TRANSFORMASI

2. Translasi (Penggeseran) Contoh Soal
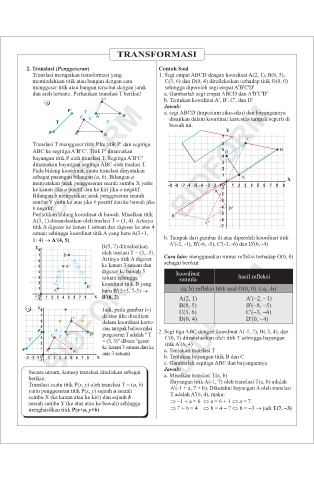
Translasi merupakan transformasi yang 1. Segi empat ABCD dengan koordinat A(2, 1), B(8, 5),
memindahkan titik atau bangun dengan cara C(3, 6) dan D(0, 4) direfleksikan terhadap titik O(0, 0)
menggeser titik atau bangun tersebut dengan jarak sehingga diperoleh segi empat A'B'C'D'
dan arah tertentu. Perhatikan translasi T berikut! a. Gambarlah segi empat ABCD dan A'B'C'D'
C¢ b. Tentukan koordinat A', B', C', dan D'
iv
BIDFORM
Jawab:
P¢ T a. segi ABCD (trapesium siku-siku) dan bayangannya
C T A¢ B¢ disajikan dalam koordinat kartesius tampak seperti di
T T
bawah ini.
Y
P A B
7
C
Translasi T menggeser titik P ke titik P¢ dan segitiga 6
ABC ke segitiga A¢B¢C¢. Titik P¢ dinamakan 5 D B
4
bayangan titik P oleh translasi T. Segitiga A¢B¢C¢ BIDFORM
dinamakan bayangan segitiga ABC oleh traslasi T. 3
Pada bidang koordinat, suatu translasi dinyatakan 2
sebagai pasangan bilangan (a, b). Bilangan a 1 A
X
menyatakan jarak penggeseran searah sumbu X yaitu O
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
ke kanan jika a positif dan ke kiri jika a negatif. A¢ -1
Bilangan b menyatakan jarak penggeseran searah -2
sumbu Y yaitu ke atas jika b positif dan ke bawah jika -3
b negatif. -4 D¢
Perhatikan bidang koordinat di bawah. Misalkan titik B¢ -5
A(3, 1) ditranslasikan oleh traslasi T = (1, 4). Artinya -6
C¢
titik A digeser ke kanan 1 satuan dan digeser ke atas 4 -7
satuan sehingga koordinat titik A yang baru A(3+1,
b. Tampak dari gambar di atas diperoleh koordinat titik
1+4) ® A¢(4, 5) A'(-2, -1), B'(-8, -5), C'(-3, -6) dan D'(0, -4)
Y B(5, 7) ditraslasikan
8
7 B oleh traslasi T = (3, -5). Cara lain: menggunakan rumus refleksi terhadap O(0, 0)
6 Artinya titik A digeser sebagai berikut
BIDFORM
BIDFORM
5 A¢ T = (3, -5) ke kanan 3 satuan dan
4 digeser ke bawah 5 koordinat
3 T = (1, 4) satuan sehingga semula hasil refleksi
2 koordinat titik B yang
1 B¢ (a, b) refleksi titik asal O(0, 0) (-a, -b)
A baru B'(5+3, 7-5) ®
-1 O 1 2 3 4 5 6 7 8 X B'(8, 2)
-1 A(2, 1) A'(-2, -1)
B(8, 5) B'(-8, -5)
iv Y
8 Jadi, pada gambar iv) C(3, 6) C'(-3, -6)
7 di atas jika disajikan
C¢ D(0, 4) D'(0, -4)
6 dalam koordinat karte-
5
P¢ 4 T sius tampak bahwa nilai 2. Segi tiga ABC dengan koordinat A(-1, 7), B(-3, 4), dan
C T A¢ B¢ pergeseran T adalah “ T
3 C(0, 3) ditranslasikan oleh titik T sehingga bayangan
T T = (3, 3)” dibaca “geser
2 titik A'(6, 4)
ke kanan 3 satuan dan ke
P 1 A B atas 3 satuan) a. Tentukan translasi T
-3 -2 -1 O 1 2 3 4 5 6 7 8 X b. Tentukan bayangan titik B dan C
-1
c. Gambarlah segitiga ABC dan bayangannya
Jawab:
Secara umum, konsep translasi dituliskan sebagai a. Misalkan translasi T(a, b)
berikut: Bayangan titik A(-1, 7) oleh translasi T(a, b) adalah
Translasi suatu titik P(x, y) oleh translasi T = (a, b)
A'(-1 + a, 7 + b). Diketahui bayangan A oleh translasi
yaitu penggeseran titik P(x, y) sejauh a searah T adalah A'(6, 4), maka:
sumbu X (ke kanan atau ke kiri) dan sejauh b
Þ -1 + a = 6 Û a = 6 + 1 Û a = 7
searah sumbu Y (ke atas atau ke bawah) sehingga
menghasilkan titik P(x+a, y+b) Þ 7 + b = 4 Û b = 4 - 7 Û b = -3 ® jadi T(7, -3)