Page 86 - ISCI’2017

do not exceed 16 bits, there is a sharp transition from very small values (almost equal to zero values

P (2 , 0) and ( , )k l ), to very large values (close to unity). This is true for the dependency
>
k
δ
P (2 , 0) , and the multiplier 2 l k− in (7) smoothes the final function (7), inverting the high-quality
k
>
form of the dependency (5).

l l

P(2 ,>0) δ (k, l)
k

k k

l
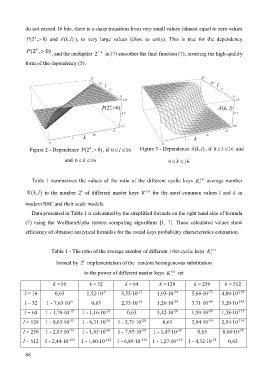
Figure 2 - Dependence (2 , 0)P k > , if 0 ≤≤ 16 Figure 3 - Dependence ( , )k lδ , if 0 ≤≤ 16 and
l
k
and 0 ≤≤ 16 0 ≤≤ 16
k

Table 1 summarizes the values of the ratio of the different cyclic keys K i ()x average number

, k
N ( ) l to the number 2 of different master keys K ()x for the most common values l and k in
k
modern BSC and their scale models.

Data presented in Table 1 is calculated by the simplified formula on the right hand side of formula
(7) using the WolframAlpha system computing algorithms [1, 7]. These calculated values show

efficiency of obtained analytical formulas for the round keys probability characteristics estimation.

Table 1 - The ratio of the average number of different l-bit cyclic keys K ()x
i
k
formed by 2 implementation of the random homogeneous substitution
to the power of different master keys K ()x set

k = 16 k = 32 k = 64 k = 128 k = 256 k = 512
-34
-5
-15
-73
l = 16 0,63 1,52∙10 3,55∙10 1,93∙10 5,66∙10 4,89∙10 -150
-29
-10
-68
-6
l = 32 1 - 7,63∙10 0,63 2,33∙10 1,26∙10 3,71∙10 3,20∙10 -145
-10
-15
-58
-20
l = 64 1 - 1,78∙10 1 - 1,16∙10 0,63 5,42∙10 1,59∙10 1,38∙10 -135
-39
-30
-35
l = 128 1 - 9,63∙10 1 - 6,31∙10 1 - 2,71∙10 0,63 2,94∙10 2,54∙10 -116
-20
-78
l = 256 1 - 2,83∙10 1 - 1,85∙10 1 - 7,97∙10 1 - 1,47∙10 0,63 8,64∙10
-59
-68
-73
-39
-78
l = 512 1 - 2,44∙10 -150 1 - 1,60∙10 -145 1 - 6,89∙10 -136 1 - 1,27∙10 -116 1 - 4,32∙10 0,63
86