Page 96 - Fiber Optic Communications Fund

Optical Fiber Transmission 77

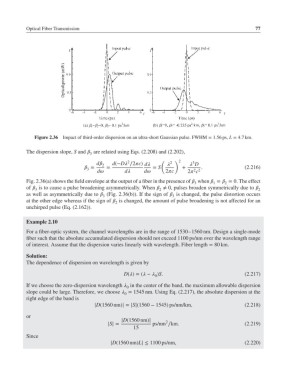
Figure 2.36 Impact of third-order dispersion on an ultra-short Gaussian pulse. FWHM = 1.56 ps, L = 4.7 km.

The dispersion slope, S and are related using Eqs. (2.208) and (2.202),
3
2
d 2 d(−D ∕2c) d ( 2 ) 2 D
3
= = = S + . (2.216)
3
2 2
d d d 2c 2 c
Fig. 2.36(a) shows the field envelope at the output of a fiber in the presence of when = = 0. The effect
3 1 2
of is to cause a pulse broadening asymmetrically. When ≠ 0, pulses broaden symmetrically due to
3 2 2
as well as asymmetrically due to (Fig. 2.36(b)). If the sign of is changed, the pulse distortion occurs
3 3
at the other edge whereas if the sign of is changed, the amount of pulse broadening is not affected for an
2
unchirped pulse (Eq. (2.162)).
Example 2.10
For a fiber-optic system, the channel wavelengths are in the range of 1530–1560 nm. Design a single-mode
fiber such that the absolute accumulated dispersion should not exceed 1100 ps/nm over the wavelength range
of interest. Assume that the dispersion varies linearly with wavelength. Fiber length = 80 km.
Solution:
The dependence of dispersion on wavelength is given by
D()=( − )S. (2.217)
0
If we choose the zero-dispersion wavelength in the center of the band, the maximum allowable dispersion
0
slope could be large. Therefore, we choose = 1545 nm. Using Eq. (2.217), the absolute dispersion at the
0
right edge of the band is
|D(1560 nm)| = |S|(1560 − 1545) ps/nm/km, (2.218)
or
|D(1560 nm)| 2
|S| = ps/nm ∕km. (2.219)
15
Since
|D(1560 nm)L| ≤ 1100 ps/nm, (2.220)