Page 41 - E-MODUL JARAK ANTAR BANGUN RUANG

√ √
√

√
√

Jadi, jarak titik ke bidang adalah √ cm

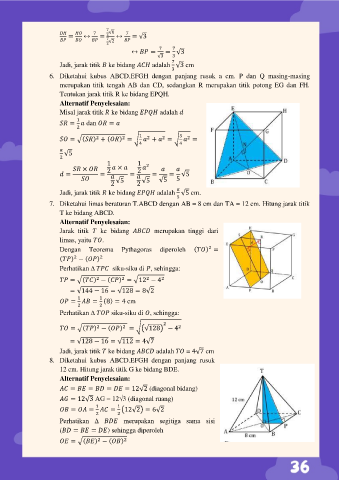
6. Diketahui kubus ABCD.EFGH dengan panjang rusuk a cm. P dan Q masing-masing
merupakan titik tengah AB dan CD, sedangkan R merupakan titik potong EG dan FH.
Tentukan jarak titik R ke bidang EPQH.
Alternatif Penyelesaian:
Misal jarak titik ke bidang adalah

dan

√( ) ( ) √ √

√

√
√ √ √

Jadi, jarak titik ke bidang adalah √ cm.

7. Diketahui limas beraturan T.ABCD dengan AB = 8 cm dan TA = 12 cm. Hitung jarak titik
T ke bidang ABCD.
Alternatif Penyelesaian:
Jarak titik ke bidang merupakan tinggi dari
limas, yaitu .

Dengan Teorema Pythagoras diperoleh ( )
( ) ( )

Perhatikan  siku-siku di , sehingga:

√( ) ( ) √

√ √ √

( ) cm

Perhatikan  siku-siku di , sehingga:

√( ) ( ) √ (√ )
√ √ √
Jadi, jarak titik ke bidang adalah = √ cm
8. Diketahui kubus ABCD.EFGH dengan panjang rusuk
12 cm. Hitung jarak titik G ke bidang BDE.
Alternatif Penyelesaian:
√ (diagonal bidang)
√ AG = 12√3 (diagonal ruang)

( √ ) √

Perhatikan  merupakan segitiga sama sisi
( ) sehingga diperoleh

√( ) ( )