Page 64 - Modul Usaha dan Energi Kelas X

56 | P a g e

TEOREMA USAHA-ENERGI

A. HUBUNGAN USAHA DENGAN ENERGI KINETIK

Sebuah benda bermassa m yang sedang bergerak pada suatu garis lurus

mendatar dengan kelajuan awav v 1. Sebuah gaya konstan F yang searah dengan

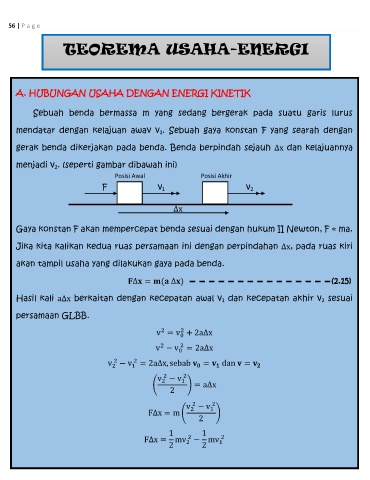
gerak benda dikerjakan pada benda. Benda berpindah sejauh ∆x dan kelajuannya

menjadi v 2. (seperti gambar dibawah ini)

Posisi Awal Posisi Akhir
F v 1 v 2

∆x

Gaya konstan F akan mempercepat benda sesuai dengan hukum II Newton, F = ma.

Jika kita kalikan kedua ruas persamaan ini dengan perpindahan ∆x, pada ruas kiri

akan tampil usaha yang dilakukan gaya pada benda.

∆ = ሺ ∆ ሻ (2.15)

Hasil kali a∆x berkaitan dengan kecepatan awal v 1 dan kecepatan akhir v 2 sesuai

persamaan GLBB.

v = v + 2a∆x
2
2
0
v − v = 2a∆x
2
2
0
v − v = 2a∆x, sebab = dan =
2
2

1
2

2
2
v − v 1
2
( ) = a∆x
2
2
v − v 1 2
2
F∆x = m ( )
2
1 1
2
2
F∆x = mv − mv
1
2
2
2