Page 20 - MODUL SISTEM KOMPUTER (YM)

banyak ditemui bila mana kita berhubungan dengan bahasa mesin yang menggunakan sistem
bilangan biner. Demikian juga bila kamu berhubungan dengan bahasa assembler, maka akan
banyak ditemui nilai yang dinyatakan dalam sistem bilangan heksadesimal ataupun sistem
bilangan octal. Angka - angka pada setiap sistem bilangan dapat dikonversikan ke dalam sistem
bilangan lain. Dalam melakukan pengkonversian diperlukan ketelitian, ketekunan, dan
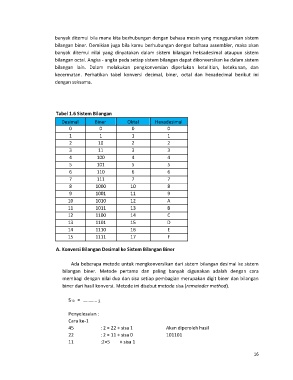
kecermatan. Perhatikan tabel konversi decimal, biner, octal dan hexadecimal berikut ini
dengan seksama.

Tabel 1.6 Sistem Bilangan

Desimal Biner Oktal Hexadesimal
0 0 0 0

1 1 1 1

2 10 2 2

3 11 3 3

4 100 4 4

5 101 5 5

6 110 6 6

7 111 7 7

8 1000 10 8

9 1001 11 9

10 1010 12 A

11 1011 13 B

12 1100 14 C

13 1101 15 D

14 1110 16 E

15 1111 17 F

A. Konversi Bilangan Desimal ke Sistem Bilangan Biner

Ada beberapa metode untuk mengkonversikan dari sistem bilangan desimal ke sistem
bilangan biner. Metode pertama dan paling banyak digunakan adalah dengan cara
membagi dengan nilai dua dan sisa setiap pembagian merupakan digit biner dan bilangan
biner dari hasil konversi. Metode ini disebut metode sisa (remainder method).

510 = ………… 2

Penyelesaian :
Cara ke-1
45 : 2 = 22 + sisa 1 Akan diperoleh hasil
22 : 2 = 11 + sisa 0 101101
11 :2=5 + sisa 1

16