Page 18 - FORMULARIO FISICA

Formulario de FÍSICA Formulario de FÍSICA

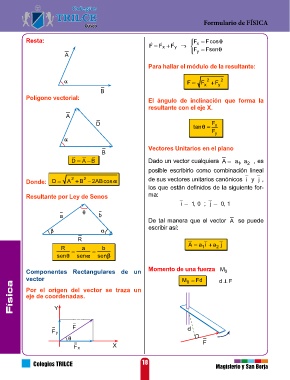
Resta: F Fcos F : Fuerza que provoca el giro. Dados dos puntos en el espacio, se pue-
F x F F y F x Fsen d : valor de brazo de momento de hallar el vector que dichos puntos
A y determinan, aplicando:
VECTORES EN EL ESPACIO
Para hallar el módulo de la resultante: V = P final P inicial
Análogamente a los puntos del plano
2
F F x 2 F cartesiano que están representados por Módulo de un vector en R 3
y
B un par ordenado, los puntos del espacio El módulo de un vector A = a i+a j+a k ;
Polígono vectorial: El ángulo de inclinación que forma la se representan mediante ternas de nú- está dado por: 1 2 3
resultante con el eje X. meros o coordenadas espaciales. 2 2 2
A Y A = a 1 +a 2 +a 3
D tan F x
F y Del gráfico:
Y
Vectores Unitarios en el plano
B cota O P(x,y,z) ordenada
D A B Dado un vector cualquiera A a , a 2 , es Z a 2
1
posible escribirlo como combinación lineal abscisa X O A
Donde: D A 2 B 2 2ABcos de sus vectores unitarios canónicos i y j , a 3 a
los que están definidos de la siguiente for- Puntos en el espacio: (x, y, z) Z 1
Resultante por Ley de Senos ma: X: eje de abscisas X
i 1, 0 ; j 0, 1 Y: eje de ordenadas
Z: eje de cotas
a b
De tal manera que el vector A se puede Y Vector Unitario
escribir así:
Dado un vector: A = (a ,a , a ), se define
1
3
2
R a como vector unitario en la dirección de
R a b A a 1 i a 2 j 2
A , a la expresión:
sen sen sen O A A
a 3 A(a ,a ,a ) U A =
1
2
3
Componentes Rectangulares de un Momento de una fuerza M 0 Z a 1 A a i+a j+a k
3
vector M 0 Fd d F X U A = a 1 1 2 +a 2 2 2 +a 3 2
Física Por el origen del vector se traza un Componentes de un vector en R 3 3 Dirección de un vector en R : Física
eje de coordenadas.
3
Expresión vectorial de un vector en R
Y
3
Un vector A = (a ,a , a ), se puede escri- La dirección de un vector en R , está
dada por sus ángulos de orientación con
1
2
3
F d bir como combinación lineal de sus vecto- respecto a los 3 ejes coordenados. Y a
F y res unitarios canónicos, así: los cosenos de dichos ángulos se
1
2
3
F x X F A = a i+a j+a k denominan cosenos directores.
Colegios TRILCE 18 Magisterio y San Borja Colegios TRILCE 19 Magisterio y San Borja