Page 156 - Secundaria - Matemáticas 3 - McGraw Hill

y5x2
Una síntesis...
Una función cuadrática expresa comportamientos que presentan cierta simetría, por ejemplo, una pelota que sube y baja; ¿podrían mencionar algunas de las caracterís- ticas de esta función? ______________________________________________________
_________________________________________________________________________
La representación gráfica de la función cuadrática se llama parábola, ¿cuál es la for- ma que tiene la parábola?, descríbanla. _______________________________, ¿pueden reconocer esta forma en algún fenómeno de su vida cotidiana?, mencionen al menos dos. ____________________________________________________________________.
LOS MÉTODOS
En las actividades se mostró que la gráfica de las funciones cuadráticas responden a un lugar geométrico llamado parábola; además, tales funciones pueden servir como modelo matemático para situaciones como el lanzamiento de una pelota y la rela- ción entre el lado de un cuadrado y su área, incluso que la misma función cuadrá- tica se puede modelar a partir de una parábola y una recta. En general, ¿qué otras características observaron de la parábola? ___________________________________
__________________________________________________________________________
Así, podemos decir que la función y 5 x2 es una función cuadrática, en la que el ex- ponente de la variable x es 2, que la función no se comporta de manera constante y que su gráfica es una parábola.
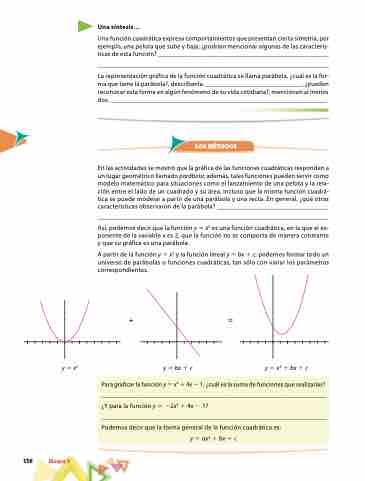
A partir de la función y 5 x2 y la función lineal y 5 bx 1 c, podemos formar todo un universo de parábolas o funciones cuadráticas, tan sólo con variar los parámetros correspondientes.
15
y5bx1c y5x2 1bx1c
Para graficar la función y 5 x2 1 4x 2 1, ¿cuál es la suma de funciones que realizarías? _________________________________________________________________________ ¿Yparalafuncióny522x2 14x21? _________________________________________________________________________ Podemos decir que la forma general de la función cuadrática es:
y5ax2 1bx1c
156 Bloque 3