Page 190 - Buku Teks Digital Mate KSSM T5

Bab 7 Graf Gerakan

Contoh 6
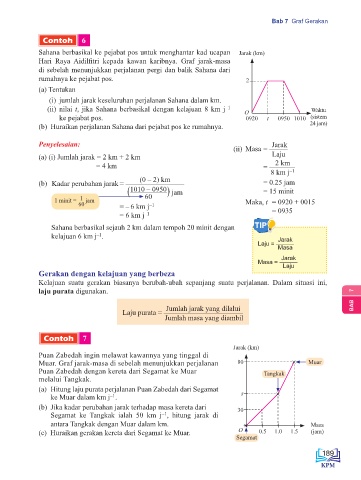
Sahana berbasikal ke pejabat pos untuk menghantar kad ucapan Jarak (km)
Hari Raya Aidilfitri kepada kawan karibnya. Graf jarak-masa
di sebelah menunjukkan perjalanan pergi dan balik Sahana dari
rumahnya ke pejabat pos. 2
(a) Tentukan
(i) jumlah jarak keseluruhan perjalanan Sahana dalam km.
–1
(ii) nilai t, jika Sahana berbasikal dengan kelajuan 8 km j O Waktu
ke pejabat pos. 0920 t 0950 1010 (sistem
(b) Huraikan perjalanan Sahana dari pejabat pos ke rumahnya. 24 jam)

Penyelesaian: Jarak
(ii) Masa = ——–
(a) (i) Jumlah jarak = 2 km + 2 km Laju
2 km
= 4 km = ———–
–1
8 km j

(0 – 2) km

(b) Kadar perubahan jarak = ———————— = 0.25 jam
1010 – 0950
(—————) jam = 15 minit
60
1
1 minit = — jam Maka, t = 0920 + 0015

60 = – 6 km j –1 = 0935
= 6 km j –1
Sahana berbasikal sejauh 2 km dalam tempoh 20 minit dengan TIP
kelajuan 6 km j . Jarak
–1
Laju = ———
Masa
Jarak
Masa = ———
Laju
Gerakan dengan kelajuan yang berbeza
Kelajuan suatu gerakan biasanya berubah-ubah sepanjang suatu perjalanan. Dalam situasi ini,
laju purata digunakan. 7
Jumlah jarak yang dilalui BAB
Laju purata = ———————————
Jumlah masa yang diambil
Contoh 7
Jarak (km)
Puan Zabedah ingin melawat kawannya yang tinggal di
Muar. Graf jarak-masa di sebelah menunjukkan perjalanan 80 Muar
Puan Zabedah dengan kereta dari Segamat ke Muar Tangkak
melalui Tangkak.
(a) Hitung laju purata perjalanan Puan Zabedah dari Segamat s
ke Muar dalam km j .
–1
(b) Jika kadar perubahan jarak terhadap masa kereta dari 30
Segamat ke Tangkak ialah 50 km j , hitung jarak di
–1
antara Tangkak dengan Muar dalam km. Masa
(jam)
(c) Huraikan gerakan kereta dari Segamat ke Muar. O 0.5 1.0 1.5 Saiz sebenar
Segamat
189