Page 3 - Buku Teks Digital Mate KSSM T5

Bab 1 Fungsi dan Persamaan Kuadratik dalam Satu Pemboleh Ubah

1 1.1 Fungsi dan Persamaan Kuadratik
BAB Apakah ungkapan kuadratik dalam satu pemboleh ubah?

Pembelajaran
Pernahkah anda melakar gerakan sebiji Standard
bola yang ditendang oleh seorang Mengenal pasti dan
pemain seperti yang ditunjukkan menerangkan ciri-ciri
dalam gambar rajah di sebelah? ungkapan kuadratik dalam
Bentuk gerakan ini dikenali sebagai satu pemboleh ubah.
bentuk parabola.
Tahukah anda, bentuk parabola ini mempunyai persamaan
tersendiri seperti persamaan garis lurus?
(Tambah Ransangan Minda 1, Jadi Ransangan Minda 1 akan jadi Ransangan Minda 2 dan
sebagainya) Rangsangan Minda 1

Ransangan Minda 1
Tujuan: Mengenal pasti dan menerangkan ciri-ciri ungkapan kuadratik dalam satu
Tujuan : Mengenal pasti dan menerangkan ciri-ciri ungkapan kuadratik dalam satu pemboleh
pemboleh ubah.
ubah
Langkah:
Langkah :
1. Berdasarkan jadual dalam langkah 3, masukkan semua ungkapan satu demi satu dalam
Imbas QR code untuk
1. Masukan ungkapan satu demi satu dalam perisian seperti di bawah menjalankan aktiviti ini
perisian geometri dinamik seperti di bawah.

Imbas QR Code untuk
menjalankan aktiviti ini.
https://www.geogebra.
org/graphing

2. Teliti graf yang diperoleh.
2. Teliti graf yang perolehi
3. Lengkapkan jadual di bawah.
3. Lengkapkan jadual di bawah
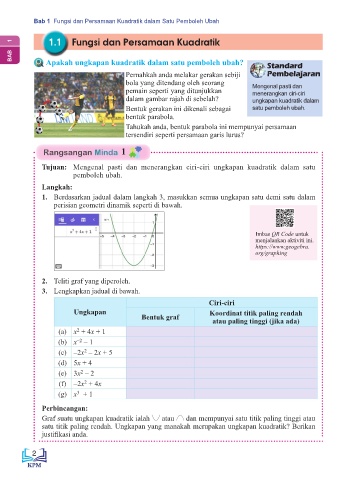
Bil Ungkapan Ciri-ciri Ciri-ciri
Bentuk graf
Ungkapan Koordinat titik paling rendah Koordinat titik paling rendah
atau paling tinggi jika ada
(a) x + 2 4x + 1 Bentuk graf atau paling tinggi (jika ada)
(a) x + 4x + 1
2
(b) x – 1
–2
(b) 1
x + 2 3x − (c) 2 –2x – 2x + 5
2
(d) 5x + 4

(c) − 2x − 2 (e) 3x 2 – 2
2x +
5
(f) –2x 2 + 4x

(g) x + 1
3
(d) 5x + 4
Perbincangan:
Graf suatu ungkapan kuadratik ialah atau dan mempunyai satu titik paling tinggi atau

satu titik paling rendah. Ungkapan yang manakah merupakan ungkapan kuadratik? Berikan
Saiz sebenar 2
justifikasi anda.

2