Page 100 - analysinew
P. 100
100
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
3. MONOTONIA ΣΥΝΑΡΤΗΣΗΣ (ΕΞΙΣΩΣΗ)
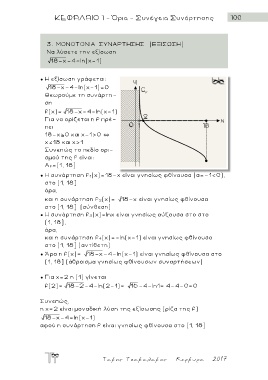
Nα λύσετε την εξίσωση
18 x-4=ln(x-1)
● Η εξίσωση γ ρ άφεται:
18 x-4-ln(x-1)=0
Θεωρούμε τη συνάρτη-
σ η
f(x)= 18 x-4-ln(x-1) (1)
Για να ορίζεται η f πρέ-
πει
18-χ 0 και χ-1>0 `
χ 18 και χ>1
Συνεπώς το πεδίο ορι-
σμού της f είναι:
Α f=(1, 18]
● H συνάρτηση f 1(x)=18-x είναι γνησίως φθίνουσα (α=-1<0),
στο (1, 18]
άρα,
και η συνάρτηση f 2(x)= 18 x είνα ι γνησίως φθίνουσα
στο (1, 18] ( σ ύνθεση)
● H συνάρτηση f 3(x)=lnx είναι γνησίως αύξουσα στο στο
(1, 18],
άρα,
και η συνάρτηση f 4(x)=-ln(x-1) είναι γνησίως φθίνουσα
στο (1, 18] (αντίθετη)
● Άρα η f(x)= 18 x-4-ln(x-1) είναι γνησίως φθίνουσα στο
(1, 18] (άθροισμα γνησίως φ θ ίνουσων συναρτήσεων)
● Για χ=2 η (1) γίνεται
f(2)= 18 2-4-ln(2-1)= 16 -4-ln1= 4-4-0=0
Συνεπώς,
η χ=2 είναι μοναδική λύση της εξίσωσης (ρίζα της f)
18 x-4=ln(x-1)
αφού η συνάρτηση f είναι γνησίως φθίνουσα στο (1, 18]
Τακης Τσακαλακος Κερκυρα 2017