Page 99 - analysinew
P. 99
99
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
2. MONOTONIA ΣΥΝΑΡΤΗΣΗΣ (ΑΝΙΣΩΣΗ)
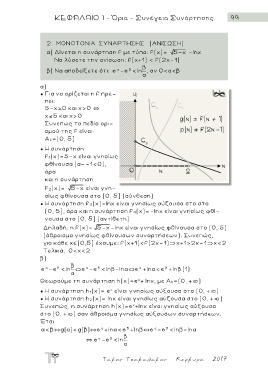
α) Δίνεται η συνάρτηση f με τύπο: f(x)= 5 x -lnx
Nα λύσετε την ανίσωση: f(x+1) < f(2x-1)
β
β
α
β) Να αποδείξετε ότι: e -e < ln α , αν 0<α<β
α )
● Για να ορίζεται η f πρέ-
πει:
5-χ 0 και χ>0 `
χ 5 και χ>0
Συνεπώς το πεδίο ορι-
σμού της f είναι:
Α f=(0, 5]
● H συνάρτηση
f 1(x)=5-x είναι γνησίω ς
φθίνουσα (α=-1<0),
άρα
και η συνάρτηση
f 2(x)= 5 x είναι γνη-
σίως φθίνουσα στο (0, 5] ( σ ύνθεση)
● H συνάρτηση f 3(x)=lnx είναι γνησίως αύξουσα στο στο
(0, 5], άρα και η συνάρτηση f 4(x)=-lnx είναι γνησίως φθί-
νουσα στο (0, 5] (αντίθετη)
Δηλαδή, η f(x)= 5 x-lnx είναι γνησίως φθίνουσα στο (0, 5]
(άθροισμα γνησίως φθίνουσων συναρτήσεων). Συνεπώς,
για κάθε χ (0,5] έχουμε: f(x+1)<f(2x-1)~x+1>2x-1~x<2
Τελικά, 0<χ<2
β )
β
e -e < ln `e -e < lnβ-lnα`e +lnα< e +lnβ (1)
α
β
α
β
α
β
α
Θεωρούμε τη συνάρτηση h(χ)=e + lnx, με Α h=(0, + )
χ
χ
● H συνάρτηση h 1(x)= e είναι γνησίως αύξουσα στο (0, + )
● H συνάρτηση h 2(x)= lnx είναι γνησίως αύξουσα στο (0, + )
Συνεπώς, η συνάρτηση h(χ)=e +lnx είναι γνησίως αύξουσα
χ
σ τ ο (0, + ) σαν άθροισμα γνησίως αύξουσων συναρτήσεων.
Έτσι
α< β`g(α)< g(β)`e +lnα< e +lnβ`e -e < lnβ-lnα
α
α
β
β
β
β
α
` e -e < ln
α
Τακης Τσακαλακος Κερκυρα 2017