Page 101 - analysinew
P. 101
101
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
4. AKΡOTATA ΣΥΝΑΡΤΗΣΗΣ
Δίνεται η συνάρτηση f με τύπο
3 2 2 3
f(x)= χ 2 1 , x 0
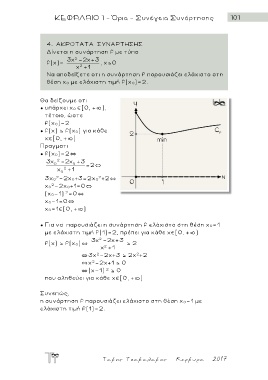
Nα αποδείξετε οτι η συνάρτηση f παρουσιάζει ελάχιστο στη
θέση χ 0 με ελάχιστη τιμή f(χ 0)=2.
Θα δείξουμε οτι
● υπάρχει χ 0 [0, + ),
τέτοιο, ώστε
f(χ 0)=2
● f(χ) f(χ 0) για κάθε
χ [0, + )
Πραγματι
● f(χ 0)=2`
3 2 2 3
0 0 =2`
2 1
0
3 χ 0 -2χ 0+3=2χ 0 +2`
2
2
χ 0 -2χ 0+1=0`
2
(χ 0-1) 2 =0`
χ 0-1=0`
χ 0=1 [0, + )
● Για να παρουσιάζει η συνάρτηση f ε λ άχιστο στη θέση χ 0=1
με ελάχιστη τιμή f(1)=2, πρέπει για κάθε χ [0, + )
3 2 2 3
f(χ) f(χ 0)` 2
2 1
`3χ -2χ+3 2χ +2
2
2
`χ -2χ+1 0
2
`(χ-1) 2 0
που αληθεύει για κάθε χ [0, + )
Συνεπώς,
η συνάρτηση f παρουσιάζει ελάχιστο στη θέση χ 0=1 με
ελάχιστη τιμή f(1)=2.
Τακης Τσακαλακος Κερκυρα 2017