Page 20 - analysinew
P. 20
20
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
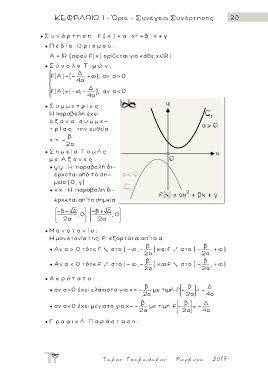
● Σ υ ν ά ρ τ η σ η f ( x ) = a ∙ x + β ∙ x + γ
2
● Π ε δ ί ο Ο ρ ι σ μ ο ύ :
Α = (αφού f(x) ορίζεται για κάθε χ )
● Σ ύ ν ο λ ο Τ ι μ ώ ν :
f(A)=[ - Δ , + ), αν α> 0
4α
f(A)=( - , - Δ ] , αν α< 0
4α
● Σ υ μ μ ε τ ρ ί ε ς :
Η παραβολή έχει
ά ξ ο ν α σ υ μ μ ε-
τ ρ ί α ς την ευθείa
β
x = -
2α
● Σ η μ ε ί α Τ ο μ ή ς
μ ε Α ξ ο ν ε ς :
● y’y : H παραβολή δ ι -
έρχεται από τo ση-
μείο (0, γ)
● x’x : H παραβολή δ ι -
έρχεται απ’τα σημεία
- β- Δ - β+ Δ
, 0 , , 0
2α 2α
● Μ ο ν ο τ ο ν ί α :
Η μον ο τονία της f εξαρτάται απ’το α.
β β
● Aν α > 0 τότε f д στο (- , - ] και f е στο [ - , + )
2α 2α
β β
● Aν α < 0 τότε f е στο (- , - ] και f д στο [ - , + )
2α 2α
● Α κ ρ ό τ α τ α :
β β Δ
● αν α>0 έχει ε λ άχιστο για χ= - με τιμή f - = -
2α 2α 4α
β β Δ
● αν α<0 έχει μέγιστο για χ= - με τιμή f - = -
2α 2α 4α
● Γ ρ α φ ι κ ή Π α ρ ά σ τ α σ η :
Τακης Τσακαλακος Κερκυρα 2017