Page 148 - chapter 1

148
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

● Τ ο όριο lim f(x) (αν αυτό υπάρχει) είναι μοναδικό.
x x 0

● Σ υ ν έ π ε ι α ο ρ ι σ μ ο ύ
● lim f(x)= L` lim [f(x)-L]= 0
x x 0 x x 0
● lim f(x)= L` lim f(x +h)= L
x x 0 h 0 0
● lim f(x)= L`lim f(x h)= L με x 0 0
x x 0 h 1 0
● Αν μία συνάρτηση f είναι
ορισμένη σ’ενα σύνολο
της μορφής
(α, x 0) ( x 0, β),
τότε ισχύει η ίσοδυναμία
lim f(x)= L `
x x 0

lim f(x)= lim f(x)= L
x x 0 - x x 0 +
● Αν μια συνάρτηση f ε ί -
ναι ορισμένη σ’ενα δ ι ά-
στημα της μορφής
(α, x 0), ενώ δεν ορίζ ε -
ται στο δι ά στημα (x 0, β),
τότε ο ρ ίζουμε

lim f(x)= lim f(x)
x x 0 x x 0 -
● Αν μια συνάρτηση f ε ί -
ναι ορισμένη σ’ενα διά-
στημα της μορφής
(x 0, β), ενω δεν ορίζεται
στο διάστημα (α, x 0),
τότε ο ρ ίζουμε

lim f(x)= lim f(x)
x x 0 x x 0 +
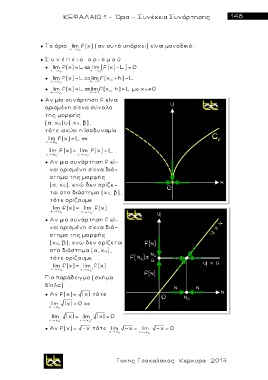
Για παράδειγμα (σχήμα
δίπλα)
● Αν f(x)= | x| τότε

lim | x| = 0 `
x x 0

lim | x| = lim | x| = 0
x x 0 - x x 0 +
● Αν f(x)= -x τότε lim -x = lim -x = 0
x x 0 x x 0 -

Τακης Τσακαλακος Κερκυρα 2017