Page 193 - chapter 1

193
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΟΡIΟ ΣΥΝΑΡΤΗΣΗΣ (ΚΡΙΤΗΡΙΟ ΠΑΡΕΜΒΟΛΗΣ)
α) H συνάρτηση f είναι ορισμένη στο και για κάθε χ
ισχύει 4χ +ημ χ+1 f(χ) συνχ+χ
2
2
Να υπολογίσετε το όριο limf(x)
x 0
β) Αν για κάθε χ>0 είναι 4 f(χ) χ+4, να βρείτε τα
● limf(x) ● lim f(x) -8
x 4 x 4 4

α )
lim (4x 2 +ημ x+1)=
2
x 0
2
= lim4x 2 + limημ x+ lim1=
x 0 x 0 x 0
= 0+0+1= 1
lim(συνx+x)
x 0
= limσυνx+ limx = 1+0= 1
x 0 x 0
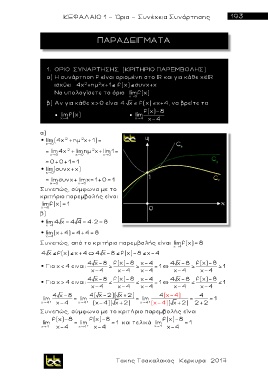
Συνεπώς, σύμφωνα με το
κριτήριο παρεμβολής είναι

limf(x)=1
x 0
β )
lim 4 x= 4 4 = 4× 2= 8
x 4
lim (x+4)= 4+4= 8
x 4
Συνεπώς, από το κριτήριο παρεμβολής είναι limf(x)=8
x 4
4 x f(x) x+4 4 x-8 f(x)-8 x-4

Για x< 4 ειναι: 4 x-8 f(x)-8 x-4 = 1 4 x-8 f(x)-8 1
x-4 x-4 x-4 x-4 x-4
Για x> 4 ειναι: 4 x-8 f(x)-8 x-4 = 1 4 x-8 f(x)-8 1
x-4 x-4 x-4 x-4 x-4

4 x-8 4( x-2)( x +2) 4 (x-4) 4
lim = lim = lim = = 1
x 4 ± x-4 x 4 ± (x-4)( x +2) x 4 ± (x-4)( x +2) 2+2
Συνεπώς, σύμφωνα με το κριτήριο παρεμβολής είναι
f(x)- 8 f(x)- 8 f(x)- 8
lim = lim =1 και τελικά lim =1
x 4 - x- 4 x 4 + x- 4 x 4 x- 4

Τακης Τσακαλακος Κερκυρα 2017