Page 269 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 269

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Το αντίστροφο του θεωρήματος (εκτός της τελευταίας)
δεν ισχύει
δηλαδή
μπορεί να ισχύει μια από τις πέντε πρώτες πράξεις και να μην
είναι απαραίτητα συνεχείς οι συναρτήσεις f και g.
Παραδείγματα

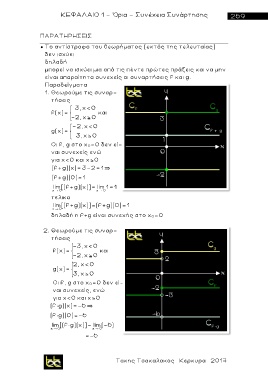
1. Θεωρούμε τις συναρ-
τήσεις
3, x<0
f(x)= και
-2, x 0
-2, x<0
g(x)=
3, x 0

Οι f, g στο χ 0=0 δεν εί-
ναι συνεχείς ε ν ώ
για χ<0 και χ 0

(f+g)(x)= 3-2= 1~
(f+g)(0)= 1

lim[(f+g)(x)]= lim 1 1
x 0 x 0
τελικα
lim[(f+g)(x)]=(f+g)(0)=1
x 0
δηλαδή η f+g είναι συνεχής στο χ 0=0

2. Θεωρούμε τις συναρ-
τήσεις
-3, x<0
f(x)= και
-2, x 0
2, x< 0
g(x)=
3, x 0
Oι f, g στο χ 0=0 δεν εί-
ναι συνεχείς, ενώ

για χ<0 και χ 0
(f g)(x)=-6 ~
(f g)(0)=-6

lim[(f g)(x)]= lim(-6)
x 0 x 0
6

Τακης Τσακαλακος Κερκυρα 2017